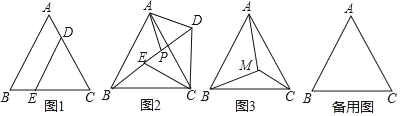
【题目】如图,边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2![]() .
.
(1)若将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD,BE,在旋转过程中,AD和BE又怎样的数量关系?并说明理由;
(2)在(1)旋转过程中,边D′E′的中点为P,连接AP,当AP最大时,求AD′的值.
(3)若点M为等边△ABC内一点,且MA=4a,MB=5a,MC=3a,求∠AMC的度数.
参考答案:
【答案】(1)AD'=BE',理由见解析;(2)2![]() ;(3)∠AMC=150°.
;(3)∠AMC=150°.
【解析】试题分析:(1)利用旋转的性质,即可判断出△ACD≌△BCE'即可得出结论;
(2)先判断出点A,C,P三点共线,先求出CP,AP,最后用勾股定理即可得出结论;
(3)将△BMC绕点C顺时针旋转得到△ANC,连接MN,只要证明△CMN是等边三角形,△AMN是Rt△即可解决问题;
试题解析:(1)结论:AD'=BE',
理由:当α≠180°时,由旋转的性质得,∠ACD'=∠BCE',
由(1)知,AC=BC,CD'=CE',
∴△ACD'≌△BCE',
∴AD'=BE';
(2)如图连接CP,
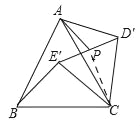
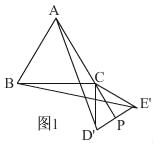
在△ACP中,由三角形三边关系得,AP<AC+CP,
∴当点A,C,P三点共线时,AP最大,
如图1,在△D'CE'中,由P为D'E的中点,得AP⊥D'E',PD'=![]() ,
,
∴CP=3,
∴AP=6+3=9,
在Rt△APD'中,由勾股定理得,AD'=![]() =2
=2![]() ;
;
(3)将△BMC绕点C顺时针旋转得到△ANC,连接MN,
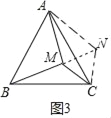
∴CM=CN,BM=AN,△BCM≌△ACN,
∵ABC是等边三角形,
∴∠ACB=60°,
∵∠ACN=∠BCM,
∴∠MCN=60°,
∴△CMN是等边三角形,
∴∠CMN=60°,MN=CM=6,
在△AMN中,∵AM2+MN2=(4a)2+(3a)2=(5a)2=AN2,
∴∠AMN=90°,
∴∠AMC=150°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )
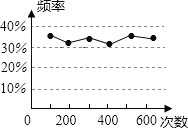
A. 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率
B. 掷一枚质地均匀的硬币,正面朝上的概率
C. 从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
D. 任意买一张电影票,座位号是2的倍数的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价2元,商场平均每天可多售出5件.求:
(1)若商场平均每天要赢利1400元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(a,0),B(0,b),C(-a,0),且
 +b2-4b+4=0.
+b2-4b+4=0.(1)求证:∠ABC=90°;
(2)∠ABO的平分线交x轴于点D,求D点的坐标.
(3)如图,在线段AB上有两动点M、N满足∠MON=45°,求证:BM2+AN2=MN2.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是( )

A.12B.12
 C.6D.6
C.6D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
物体的质量(kg)
0
1
2
3
4
5
弹簧的长度(cm)
12
12.5
13
13.5
14
14.5
(1)上表反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度怎样变化?
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(5)当物体的质量为2.5kg时,根据(4)的关系式,求弹簧的长度.
相关试题

