【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价2元,商场平均每天可多售出5件.求:
(1)若商场平均每天要赢利1400元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
参考答案:
【答案】(1)20;(2)当每件衬衫降价16元时,专卖店每天获得的利润最大,最大利润是1440元
【解析】试题分析:(1)设每件衬衫降价x元,根据题意列出方程,解方程即可得到x的值;
(2)用“配方法”即可求出y的最大值,即可得到每件衬衫降价多少元.
试题解析:(1)设每件衬衫降价x元,
则(40﹣x)(20+![]() x)=1400,
x)=1400,
解得 x1=12,x2=20,
经检验,x1=10,x2=20都是原方程的解,但要尽快减少库存,
所以x=20,
答:每件衬衫应降价20元;
(2)设每件衬衫降价x元,商场平均每天盈利y元,
∵y=(40﹣x)(20+![]() x)=﹣
x)=﹣![]() (x﹣16)2+1440,
(x﹣16)2+1440,
∴当x=16时,y的最大值为1440,
答:当每件衬衫降价16元时,专卖店每天获得的利润最大,最大利润是1440元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3 cm/s的速度向点B移动,一直到达点B为止;点Q以2 cm/s的速度向点D移动。经过长时间P、Q两点之间的距离是10 cm?(8′)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,BC=2AB,M是AD的中点,CE⊥AB,垂足为E,求证:∠DME=3∠AEM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在一次用频率估计概率的实验中,统计了某一结果出现的频率,并绘制了如图所示的统计图,则符合这一结果的实验可能是( )
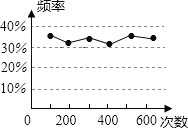
A. 从一个装有2个白球和1个红球的不透明袋子中任意摸出一球(小球除颜色外,完全相同),摸到红球的概率
B. 掷一枚质地均匀的硬币,正面朝上的概率
C. 从一副去掉大小王的扑克牌,任意抽取一张,抽到黑桃的概率
D. 任意买一张电影票,座位号是2的倍数的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(a,0),B(0,b),C(-a,0),且
 +b2-4b+4=0.
+b2-4b+4=0.(1)求证:∠ABC=90°;
(2)∠ABO的平分线交x轴于点D,求D点的坐标.
(3)如图,在线段AB上有两动点M、N满足∠MON=45°,求证:BM2+AN2=MN2.


-
科目: 来源: 题型:
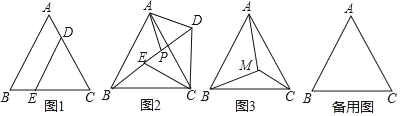
查看答案和解析>>【题目】如图,边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2
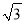 .
.(1)若将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD,BE,在旋转过程中,AD和BE又怎样的数量关系?并说明理由;
(2)在(1)旋转过程中,边D′E′的中点为P,连接AP,当AP最大时,求AD′的值.
(3)若点M为等边△ABC内一点,且MA=4a,MB=5a,MC=3a,求∠AMC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求
 的值.
的值.
相关试题

