【题目】已知:△ABC是等边三角形.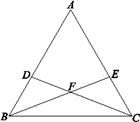
(1)如图,点D在AB边上,点E在AC边上,BD=CE,BE与CD交于点F. 试判断BF与CF的数量关系,并加以证明;
(2)点D是AB边上的一个动点,点E是AC边上的一个动点,且BD=CE,BE与CD交于点F.若△BFD是等腰三角形,求∠FBD的度数.
参考答案:
【答案】
(1)解:BF=CF;理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
在△BCD和△CBE中, 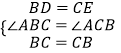 ,
,
∴△BCD≌△CBE(SAS),
∴∠BCD=∠CBE,
∴BF=CF.
(2)解:由(1)得:∠BCD=∠CBE,∠ACB=60°,
设∠BCD=∠CBE=x,
∴∠DBF=60°﹣x,
若△BFD是等腰三角形,分三种情况:
①若FD=FB,则∠FBD=∠FDB>∠A,
∴∠FBD=∠FDB>60°,
但∠FBD>∠ABC,
∴∠FBD<60°,
∴FD=FB的情况不存在;
②若DB=DF,则∠FBD=∠BFD=2x,
∴60°﹣x=2x,
解得:x=20°,
∴∠FBD=40°;
③若BD=BF,如图所示: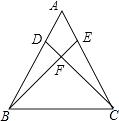
则∠BDF=∠BFD=2x,
在△BDF中,∠DBF+∠BDF+∠BFD=180°,
∴60°﹣x+2x+2x=180°,
解得:x=40°,
∴∠FBD=20°;
综上所述:∠FBD的度数是40°或20°.
【解析】(1)根据题意再由SAS证明△BCD≌△CBE,再由全等三角形的性质可证得结论;
(2)△BFD是等腰三角形,分三种情况:①若FD=FB;②若DB=DF;③若BD=BF,根据三角形的内角和可求出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程3x+y=4化为用x的式子表示y的形式为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
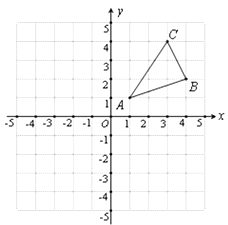
⑴ 作出与△ABC关于y轴对称△A1B1C1 , 并写出三个顶点的坐标为:A1(),B1(),C1(); -
科目: 来源: 题型:
查看答案和解析>>【题目】今年某市高中招生体育考试测试管理系统的运行,将测试完进行换算统分改为计算机自动生成,现场公布成绩,降低了误差,提高了透明度,保证了公平.考前张老师为了解全市初三男生考试项目的选择情况(每人限选一项),对全市部分初三男生进行了调查,将调查结果分成五类:
 、实心球(
、实心球(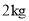 );
);  、立定跳远;
、立定跳远;  、
、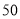 米跑;
米跑;  、半场运球;
、半场运球;  、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: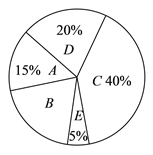

(
 )将上面的条形统计图补充完整.
)将上面的条形统计图补充完整.(
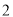 )假定全市初三毕业学生中有
)假定全市初三毕业学生中有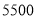 名男生,试估计全市初三男生中选
名男生,试估计全市初三男生中选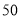 米跑的人数有多少人?
米跑的人数有多少人?(
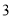 )甲、乙两名初三男生在上述选择率较高的三个项目:
)甲、乙两名初三男生在上述选择率较高的三个项目: 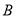 、立定跳远;
、立定跳远; 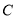 、
、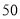 米跑;
米跑; 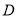 、半场运球中各选一项,同时选择半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
、半场运球中各选一项,同时选择半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-2)2019+22018的结果是 ( )
A. -22018B. 22018C. 22019D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①解分式方程一定会产生增根;
②方程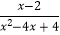 =0的根为x=2;
=0的根为x=2;
③方程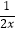 =
= 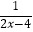 中各分式的最简公分母为2x(2x-4);
中各分式的最简公分母为2x(2x-4);
④x+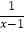 =1+
=1+ 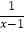 是分式方程.
是分式方程.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】初三(1)班要从甲、乙、丙、丁这
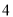 名同学中随机选取
名同学中随机选取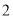 名同学参加学校毕业生代表座谈会.求下列事件的概率:
名同学参加学校毕业生代表座谈会.求下列事件的概率:(
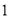 )已确定甲参加,另外
)已确定甲参加,另外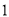 人恰好选中乙;
人恰好选中乙;(
 )随机选取
)随机选取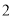 名同学,恰好选中甲和乙.
名同学,恰好选中甲和乙.
相关试题

