【题目】如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R,S,若AQ=PQ,PR=PS,则下列四个结论:①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP,其中结论正确的序号为( ) 
A.①②③
B.①②④
C.②③④
D.①②③④
参考答案:
【答案】D
【解析】解:∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2﹣PR2 , AS2=AP2﹣PS2 ,
∵AP=AP,PR=PS,
∴AR=AS,∴②正确;
∵AQ=QP,
∴∠QAP=∠QPA,
∵∠QAP=∠BAP,
∴∠QPA=∠BAP,
∴QP∥AR,∴③正确;
∵△ABC是等边三角形,
∴∠B=∠CAB=60°,AB=AC,
∵∠QAP=∠BAP,
∴BP=CP,
∵QP∥AB,
∴∠QPC=∠B=60°=∠C,
∴PQ=CQ,
∴△PQC是等边三角形,
∴PQ=CP=BP,∠SQP=60°=∠B,
∵PR⊥AB,PS⊥AC,
∴∠BRP=∠PSQ=90°,
在△BRP和△QSP中,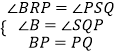 ,
,
∴△BRP≌△QSP,∴④正确;
连接RS,
∵PR=PS,
∴点P在RS的垂直平分线上,
∵AS=AR,
∴点A在RS的垂直平分线上,
∴AP垂直平分RS,∴①正确.
故答案为:①②③④.
根据角平分线性质即可推出②,根据勾股定理即可推出AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出QP∥AB即可;求出PQ=CP=BP,根据AAS推出△BRP≌△QSP即可,然后根据线段垂直平分线的判定即可得到AP垂直平分RS.
-
科目: 来源: 题型:
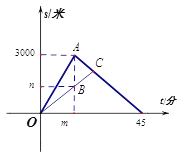
查看答案和解析>>【题目】小明和爸爸周末到湿地公园进行锻炼,两人上午9:00从公园入口出发,沿相同路线匀速运动,小明15分钟后到达目的地,此时爸爸距出发地1200米,小明到达目的地后立即按原路匀速返回,与爸爸相遇后,和爸爸一起从原路返回出发地.小明、爸爸在锻炼过程中离出发地的路程与小明出发的时间的函数关系如图.
(1)图中
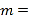 ,
, 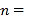 ;
;(2)求小明和爸爸相遇的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用下列图形不能进行平面镶嵌的是( )
A.正三角形和正四边形
B.正三角形和正六边形
C.正四边形和正八边形
D.正四边形和正十二边形 -
科目: 来源: 题型:
查看答案和解析>>【题目】将多项式2x3y﹣4y2+3x2﹣x按x的降幂排列为: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
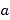 的菱形ABCD的顶点D在反比例函数
的菱形ABCD的顶点D在反比例函数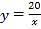 (
(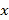 >0)的图象上,A点的坐标为(0,4),连接BD,交
>0)的图象上,A点的坐标为(0,4),连接BD,交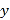 轴于点P.
轴于点P.(1)求菱形边长
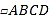 及点C坐标;
及点C坐标;(2)
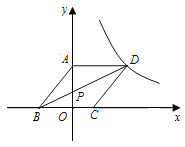 沿着线段BD平移,当点C落在
沿着线段BD平移,当点C落在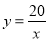 (
(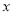 >0)上时,求点B沿BD方向移动的距离.
>0)上时,求点B沿BD方向移动的距离.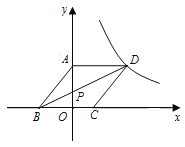
-
科目: 来源: 题型:
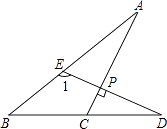
查看答案和解析>>【题目】如图,已知∠A=20°,∠B=27°,AC⊥DE,求∠1,∠D的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.求证:
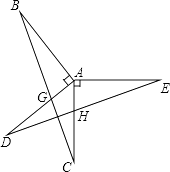
(1)△ABC≌△ADE;
(2)BC⊥DE.
相关试题

