【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若![]() ,则3S△EDH=13S△DHC,其中结论正确的有________(填写序号).
,则3S△EDH=13S△DHC,其中结论正确的有________(填写序号).

参考答案:
【答案】① ② ③
【解析】试题解析:①∵四边形ABCD为正方形,EF∥AD,
∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF-GF,DF=CD-FC,
∴EG=DF,故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=![]() ∠GFC=45°=∠HCD,
∠GFC=45°=∠HCD,
在△EHF和△DHC中,
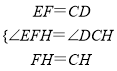 ,
,
∴△EHF≌△DHC(SAS),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=∠AEF+∠ADF=180°,故②正确;
③∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=![]() ∠GFC=45°=∠HCD,
∠GFC=45°=∠HCD,
在△EHF和△DHC中,
 ,
,
∴△EHF≌△DHC(SAS),故③正确;
④错误,当![]() ,则3S△EDH=13S△DHC,
,则3S△EDH=13S△DHC,
理由如下:∵![]() ,
,
∴AE=2BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中,
 ,
,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
过H点作HM垂直于CD于M点,如图所示:
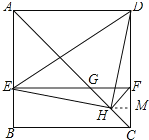
设HM=x,则DM=5x,DH=![]() x,CD=6x,
x,CD=6x,
则S△DHC=![]() ×HM×CD=3x2,S△EDH=
×HM×CD=3x2,S△EDH=![]() ×DH2=13x2,
×DH2=13x2,
∴3S△EDH=13S△DHC,故④错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列是小朋友用火柴棒拼出的一组图形:

仔细观察,找出规律,解答下列各题:
(1)第四个图中共有 根火柴棒,第六个图中共有 根火柴棒;
(2)按照这样的规律,第n个图形中共有 根火柴棒(用含n的代数式表示);
(3)按照这样的规律,第20个图形中共有多少根火柴棒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y=
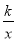 的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )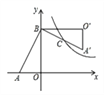
A. 20 B. 22 C. 24 D. 26
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形,若线段EF的中点为点M,则线段AM的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α与∠β互余,且∠α:∠β=3:2,那么∠α的度数是( )
A. 54° B. 36° C. 72° D. 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程3x2﹣5x=﹣3二次项系数是___,一次项系数是___,常数项是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
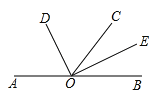
(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=a°,求∠DOE的度数;
(3)图中是否有互余的角?若有请写出所有互余的角.
相关试题

