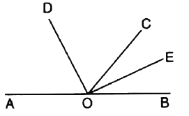
【题目】如图,点A、B在同一条直线上,OD、OE分别平分∠AOC和∠BOC.(1)求∠DOE的度数;(2)如果∠COD=65°,求∠AOE的度数.
参考答案:
【答案】(1)90°;(2)155°.
【解析】
(1)由已知条件和观察图形,再利用角平分线的性质就可求出角的度数;
(2)由已知条件和观察图形,再利用角平分线的性质就可求出角的度数.
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC,
∠AOC,
又因为OE是∠BOC的平分线,
所以∠COE=![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB=90°.
∠AOB=90°.
(2)由(1)可知,∠BOE=∠COE=90°-∠COD=25°.
所以∠AOE=∠AOB-∠BOE=155°.
故答案为:(1)90°;(2)155°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种规律下去,第n次移动到点An,如果点An,与原点的距离不少于20,那么n的最小值是( )

A. 11B. 12C. 13D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=20°,则∠AOP的度数为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校数学课外活动小组在学习了锐角三角函数后,组织了一次利用自制的测角仪测量古塔高度的活动.具体方法如下:在古塔前的平地上选择一点E,某同学站在E点用测角仪测得古塔顶的仰角为30°,从E向着古塔前进12米后到达点F,又测得古塔顶的仰角为45°,并绘制了如图的示意图(图中线段AE=BF=1.6米,表示测角的学生眼睛到地面的高度).请你帮着计算古塔CD的高度(结果保留整数,参考数据:
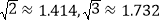 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好地服务学生,了解学生对学校管理的意见和建议,该校团委发起了“我给学校提意见”的活动,某班团支部对该班全体团员在一个月内所提意见的条数的情况进行了统计,并制成了如下两幅不完整的统计图:
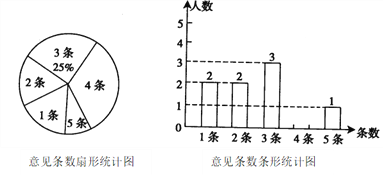
(1)该班的团员有 名,在扇形统计图中“2条”所对应的圆心角的度数为 ;
(2)求该班团员在这一个月内所提意见的平均条数是多少?并将该条形统计图补充完整;
(3)统计显示提3条意见的同学中有两位女同学,提4条意见的同学中也有两位女同学.现要从提了3条意见和提了4条意见的同学中分别选出一位参加该校团委组织的活动总结会,请你用列表或画树状图的方法,求出所选两位同学恰好是一位男同学和一位女同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一个种植总面积为
 的矩形塑料温棚,分垄间隔套种草莓和西红柿共
的矩形塑料温棚,分垄间隔套种草莓和西红柿共 垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过
垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过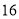 垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
垄(垄数为正整数),它们的占地面积、产量、利润分别如下:⑴若设草莓共种植了
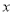 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?⑵在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
占地面积(m2/垄)
产量(千克/垄)
利润(元/千克)
西红柿
32
160
1.0
草莓
15
50
1.6
相关试题

