【题目】如图,抛物线![]() 与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
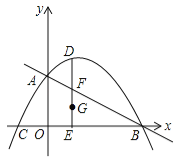
(1)求此抛物线的解析式,
(2)在DE上作点G,使G点与D点关于F点对称,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,求G点的横坐标.
参考答案:
【答案】(1)![]() ;(2)2或
;(2)2或![]() .
.
【解析】
试题分析:
(1)根据B,C两点在抛物线上,代入抛物线得到方程组,求出a,b的值即可;
(2)先求出直线AB的解析式为![]() ,设F点的坐标为(x,
,设F点的坐标为(x,![]() ),则D点的坐标为(x,
),则D点的坐标为(x,![]() ),根据G点与D点关于F点对称,所以G点的坐标为(x,
),根据G点与D点关于F点对称,所以G点的坐标为(x,![]() ),若以G为圆心,GD为半径作圆,使得⊙G与其中一条坐标轴相切,分两种情况试题解析:①若⊙G与x轴相切则必须由DG=GE;②若⊙G与y轴相切则必须由DG=OE.
),若以G为圆心,GD为半径作圆,使得⊙G与其中一条坐标轴相切,分两种情况试题解析:①若⊙G与x轴相切则必须由DG=GE;②若⊙G与y轴相切则必须由DG=OE.
试题解析:
解:(1)∵B,C两点在抛物线![]() 上,
上,
∴![]() ,解得:
,解得: .
.
∴所求的抛物线为:![]() ;
;
(2)抛物线![]() ,则点A的坐标为(0,2),
,则点A的坐标为(0,2),
设直线AB的解析式为![]() ,
,
∴![]() ,解得:
,解得: ,
,
∴直线AB的解析式为![]() ,
,
设F点的坐标为(x,![]() ),则D点的坐标为(x,
),则D点的坐标为(x,![]() ),
),
∵G点与D点关于F点对称,
∴G点的坐标为(x,![]() ),
),
若以G为圆心,GD为半径作圆,使得⊙G与其中一条坐标轴相切,
①若⊙G与x轴相切则必须有DG=GE,
即:![]() =
=![]() ,
,
即:![]() ,
,
解得:![]() ,
,![]() (舍去);
(舍去);
②若⊙G与y轴相切则必须由DG=OE,
即![]() ,
,
解得:![]() ,
,![]() (舍去);
(舍去);
综上,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,G点的横坐标为2或![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 两边分别相等的两个三角形全等
B. 两边及一角分别相等的两个三角形全等
C. 两角及一边分别相等的两个三角形全等
D. 三个角分别相等的两个三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个数的和是负数,那么这两个数( )
A.同是正数
B.同为负数
C.至少有一个为正数
D.至少有一个为负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】写出两组直角三角形的三边长________________.(要求都是勾股数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)仔细观察,在图2中有 个以线段AC为边的“8字形”;
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP=
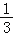 ∠CAB,∠CDP=
∠CAB,∠CDP=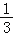 ∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
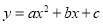 的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.
的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y轴交于点C,顶点为D.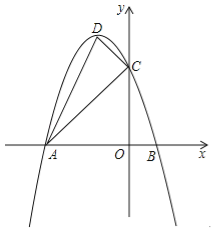
(1)求顶点D的坐标.(用含a的代数式表示);
(2)若△ACD的面积为3.
①求抛物线的解析式;
②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
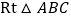 中,
中, ,
,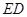 是
是 的垂直平分线,交
的垂直平分线,交 于点
于点 ,交
,交 于点
于点 .
.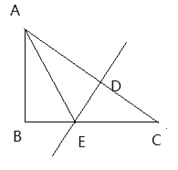
(1)、若∠BAE=200,求
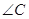 的度数。(2)、若AB=6,AC=10,求BE的长。
的度数。(2)、若AB=6,AC=10,求BE的长。
相关试题

