【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本![]() (单位:元)、销售价
(单位:元)、销售价![]() (单位:元)与产量x(单位:kg)之间的函数关系.
(单位:元)与产量x(单位:kg)之间的函数关系.
(1)请解释图中点D的横坐标、纵坐标的实际意义;
(2)求线段AB所表示的![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?

参考答案:
【答案】(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;(2)y=﹣0.2x+60(0≤x≤90);(3)当该产品产量为75kg时,获得的利润最大,最大值为2250.
【解析】
试题分析:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可;
(3)利用总利润=单位利润×产量列出有关x的二次函数,求得最值即可.
试题解析:(1)点D的横坐标、纵坐标的实际意义:当产量为130kg时,该产品每千克生产成本与销售价相等,都为42元;
(2)设线段AB所表示的![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,∵
,∵![]() 的图象过点(0,60)与(90,42),∴
的图象过点(0,60)与(90,42),∴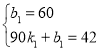 ,∴解得:
,∴解得: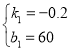 ,
,
∴这个一次函数的表达式为:y=﹣0.2x+60(0≤x≤90);
(3)设![]() 与x之间的函数关系式为
与x之间的函数关系式为![]() ,
,
∵经过点(0,120)与(130,42),∴![]() ,解得:
,解得:![]() ,
,
∴这个一次函数的表达式为![]() (0≤x≤130),
(0≤x≤130),
设产量为xkg时,获得的利润为W元,
当0≤x≤90时,W=![]() =
=![]() ,
,
∴当x=75时,W的值最大,最大值为2250;
当90≤x130时,W=![]() =
=![]() ,
,
∴当x=90时,W=![]() ,
,
由﹣0.6<0知,当x>65时,W随x的增大而减小,∴90≤x≤130时,W≤2160,
因此当该产品产量为75kg时,获得的利润最大,最大值为2250.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
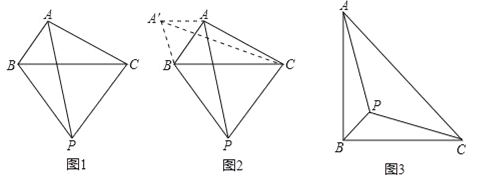
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
(1)请你回答:AP的最大值是 .
(2)参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,请写出求AP+BP+CP的最小值长的解题思路.
提示:要解决AP+BP+CP的最小值问题,可仿照题目给出的做法.把△ABP绕B点逆时针旋转60,得到△A′BP′.
①请画出旋转后的图形
②请写出求AP+BP+CP的最小值的解题思路(结果可以不化简).
-
科目: 来源: 题型:
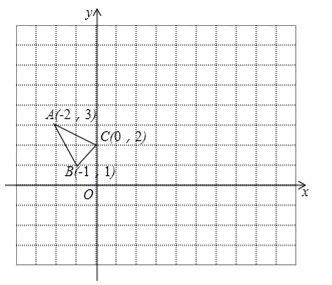
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示.(不写解答过程,直接写出结果)
(1)若△A1B1C1与△ABC关于原点O成中心对称,则点A1的坐标为 ;
(2)将△ABC向右平移4个单位长度得到△A2B2C2,则点B2的坐标为 ;
(3)将△ABC绕O点顺时针方向旋转90°,则点C走过的路径长为 ;
(4)在x轴上找一点P,使PA+PB的值最小,则点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是真命题的有( )
①直径是圆中最大的弦;②长度相等的弧是等弧;③平分弦的直径垂直于弦,并且平分弦所对的两条弧;④两个圆心角相等,它们所对的弦也相等;⑤等弧所对的圆心角相等.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(-12)-5+(-14)-(-39)
(2)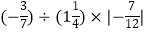
(3)-22-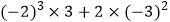
(4)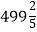 ×(-15)(用简便方法计算)
×(-15)(用简便方法计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:

请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件200元,按标价打八折售出后每件可获利40元,则该商品的标价为每件_______元。
相关试题

