【题目】已知如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠A=22.5°,CD=8cm,求⊙O的半径. 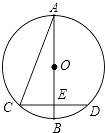
参考答案:
【答案】解:连接OC,如图所示:
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE= ![]() CD=4cm,
CD=4cm,
∵∠A=22.5°,
∴∠COE=2∠A=45°,
∴△COE为等腰直角三角形,
∴OC= ![]() CE=4
CE=4 ![]() cm,
cm,
即⊙O的半径为4 ![]() cm.
cm.
【解析】连接OC,由圆周角定理得出∠COE=45°,根据垂径定理可得CE=DE=4cm,证出△COE为等腰直角三角形,利用特殊角的三角函数可得答案.
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.
-
科目: 来源: 题型:
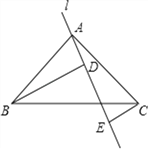
查看答案和解析>>【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:已知a+b=﹣4,ab=3,求a2+b2的值.
解:∵a+b=﹣4,ab=3,
∴a2+b2=(a+b)2﹣2ab=(﹣4)2﹣2×3=10.
请你根据上述解题思路解答下面问题:
(1)已知a﹣b=﹣3,ab=﹣2,求(a+b)(a2﹣b2)的值.
(2)已知a﹣c﹣b=﹣10,(a﹣b)c=﹣12,求(a﹣b)2+c2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
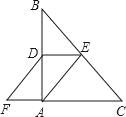
A. 16 B. 20 C. 18 D. 22
-
科目: 来源: 题型:
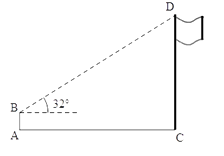
查看答案和解析>>【题目】如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°= 0.53,cos32°= 0.85,tan32°= 0.62)
相关试题

