【题目】如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,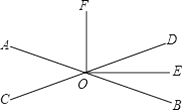
(1)求∠DOE的度数;
(2)若OF⊥OE,求∠COF的度数.
参考答案:
【答案】
(1)解:∵两直线AB,CD相交于点O,∠AOC:∠AOD=3:7,
∴∠AOC=180°× ![]() =54°,
=54°,
∴∠BOD=54°,
又∵OE平分∠BOD,
∴∠DOE=54°÷2=27°;
(2)解:∵OF⊥OE,∠DOE=27°,
∴∠DOF=63°,
∠COF=180°-63°=117°.
【解析】(1)根据平角的定义和∠AOC:∠AOD=3:7,可求出∠AOC的度数,再由对顶角相等可得∠BOD的度数,然后由角平分线的定义可求出∠DOE的度数;
(2)OF⊥OE,可得∠EOF=90° ,进而可求出∠DOF的度数,再由∠COF+∠DOF=180°可求出∠COF的度数.
【考点精析】本题主要考查了角的平分线和角的运算的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D是弧AE上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF·DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长.
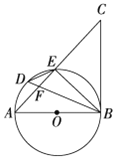
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种铂金饰品在甲、乙两种商店销售,甲店标价每克477元,按标价出售,不优惠.乙店标价每克530元,但若买的铂金饰品重量超过3克,则超出部分可打八折出售.若购买的铂金饰品重量为x克,其中x>3.
(1)分别列出到甲、乙商店购买该种铂金饰品所需费用(用含x的代数式表示);
(2)李阿姨要买一条重量10克的此中铂金饰品,到哪个商店购买最合算. -
科目: 来源: 题型:
查看答案和解析>>【题目】当k= 时,二次三项式x2﹣kx+12分解因式的结果是(x﹣4)(x﹣3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把195张图片平均分给若干名学生,已知每人分得的图片数比人数少2.学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b中,k<0,b<0,则函数不经过下列选项中的那个象限( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x2+nx+3)(x2﹣3x+m)展开式中不含x2和x3项,求(n﹣m)n的值.
相关试题

