【题目】★如图,在平面直角坐标系xOy中,直线y=![]() x-2
x-2![]() 与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
(1)判断原点O与⊙P的位置关系,并说明理由;
(2)当⊙P过点B时,求⊙P被y轴所截得的劣弧的长;
(3)当⊙P与x轴相切时,求出切点的坐标.

参考答案:
【答案】(1)见解析 (2)![]() (3)
(3) 或
或
【解析】试题分析:(1)由直线y=![]() 与x轴、y轴分别交于A,B两点,可求得点A与点B的坐标,继而求得∠OBA=30°,然后过点O作OH⊥AB于点H,利用三角函数可求得OH的长,根据直线与圆的位置关系即可得出答案;
与x轴、y轴分别交于A,B两点,可求得点A与点B的坐标,继而求得∠OBA=30°,然后过点O作OH⊥AB于点H,利用三角函数可求得OH的长,根据直线与圆的位置关系即可得出答案;
(2)当⊙P过点B时,点P在y轴右侧时,易得⊙P被y轴所截的劣弧所对的圆心角为:180°-30°-30°=120°,则可求得弧长;同理可求得当⊙P过点B时,点P在y轴左侧时,⊙P被y轴所截得的劣弧的长;
(3)首先求得当⊙P与x轴相切时,且位于x轴下方时,点D的坐标,然后利用对称性可以求得当⊙P与x轴相切时,且位于x轴上方时,点D的坐标.
试题解析:解:(1)原点O在⊙P外.理由如下:
∵直线y=![]() x-2
x-2![]() 与x轴、y轴分别交于A,B两点,
与x轴、y轴分别交于A,B两点,
∴点A的坐标为(2,0),点B的坐标为(0,-2![]() ).
).
在Rt△OAB中,tan∠OBA=![]() =
=![]() =
=![]() ,
,
∴∠OBA=30°.
如图①,过点O作OH⊥AB于点H,
在Rt△OBH中,OH=OB·sin∠OBA=![]() .
.
∵![]() >1,
>1,
∴原点O在⊙P外;
(2)如图②,当⊙P过点B时,点P在y轴右侧时,
∵PB=PC,
∴∠PCB=∠OBA=30°,
∴⊙P被y轴所截的劣弧所对的圆心角的度数为180°-30°-30°=120°,
∴弧长为![]() =
=![]() ;
;
同理:当⊙P过点B时,点P在y轴左侧时,弧长同样为![]() .
.
∴当⊙P过点B时,⊙P被y轴所截得的劣弧的长为![]() ;
;
(3)如图③,当⊙P与x轴相切时,且位于x轴下方时,设切点为D,作PD⊥x轴,
∴PD∥y轴,
∴∠APD=∠ABO=30°.
在Rt△DAP中,AD=DP·tan∠DPA=1×tan30°=![]() ,
,
∴OD=OA-AD=2-![]() ,
,
∴此时点D的坐标为![]() ;
;
当⊙P与x轴相切时,且位于x轴上方时,根据对称性可以求得此时切点的坐标为![]() .
.
综上所述,当⊙P与x轴相切时,切点的坐标为![]() 或
或![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初一年段举行科技创新比赛活动,各班选送的学生数分别为3,2,2,6,6,5,则这组数据的平均数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了测算一块600亩试验田里新培育的杂交水稻的产量,随机对其中的10亩杂交水稻的产量进行了检测,在这个问题中10是( )
A.个体
B.总体
C.总体的样本
D.样本容量 -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2m2﹣8= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
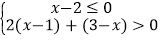 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.【答案】﹣1<x≤2,数轴表示见解析.
【解析】试题分析:分别求出不等式组中两个不等式的解集,再求出其公共解集,然后在数轴上表示出其解集.

由①得,x≤2,
由②得,x>﹣1,
故此不等式组的解集为:﹣1<x≤2.
在数轴上表示为:
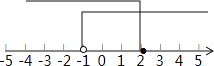
点睛: 本题考查了一元一次不等式组的解法及解集的数轴表示,先分别解两个不等式,求出它们的解集,再求两个不等式解集的公共部分.不等式组解集的确定方法是:同大取大,同小取小,大小小大取中间,大大小小无解.在数轴上空心圈表示不包含该点,实心点表示包含该点.
【题型】解答题
【结束】
22【题目】解不等式组:
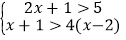 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一种细胞的直径约为0.000 052米,将0.000 052用科学记数法表示为 .
相关试题

