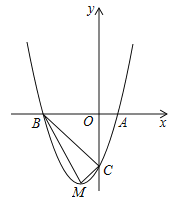
【题目】如图,顶点为M的抛物线y=a(x+1)2-4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)△BCM是直角三角形;(3)N(
;(2)△BCM是直角三角形;(3)N(![]() ,
, ![]() )或N(
)或N(![]() ,
, ![]() )或N(﹣2,﹣3).
)或N(﹣2,﹣3).
【解析】试题分析:(1)用待定系数法求出抛物线解析式即可;
(2)由抛物线解析式确定出抛物线的顶点坐标和与x轴的交点坐标,用勾股定理的逆定理即可;
(3)根据题意判断出点N只能在x轴上方的抛物线上,由已知四边形的面积相等转化出S△ABN=S△BCM,然后求出三角形BCM的面积,再建立关于点N的坐标的方程求解即可.
试题解析:(1)∵抛物线![]() 与y轴相交于点C(0,﹣3),∴﹣3=a﹣4,∴a=1,∴抛物线解析式为
与y轴相交于点C(0,﹣3),∴﹣3=a﹣4,∴a=1,∴抛物线解析式为![]() ,即
,即![]() ;
;
(2)△BCM是直角三角形.理由:
由(1)有,抛物线解析式为![]() ,∵顶点为M的抛物线
,∵顶点为M的抛物线![]() ,∴M(﹣1,﹣4),由(1)抛物线解析式为
,∴M(﹣1,﹣4),由(1)抛物线解析式为![]() ,令y=0,∴
,令y=0,∴![]() ,∴
,∴![]() =﹣3,
=﹣3, ![]() =1,∴A(1,0),B(﹣3,0),∴
=1,∴A(1,0),B(﹣3,0),∴![]() =9+9=18,
=9+9=18, ![]() =1+1=2,
=1+1=2, ![]() =4+14=20,∴
=4+14=20,∴![]() ,∴△BCM是直角三角形;
,∴△BCM是直角三角形;
(3)存在.∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,且点M是抛物线的顶点,分两种情况讨论:
①点N在x轴上方的抛物线上,如图,由(2)有△BCM是直角三角形, ![]() =18,
=18, ![]() =2,∴BC=
=2,∴BC=![]() ,CM=
,CM=![]() ,∴S△BCM=
,∴S△BCM=![]() BC×CM=
BC×CM=![]() =3,设N(m,n),∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,∴S△ABN+S△ABC=S△BCM+S△ABC,∴S△ABN=S△BCM=3,∵A(1,0),B(﹣3,0),∴AB=4,∴S△ABN=
=3,设N(m,n),∵以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等,∴S△ABN+S△ABC=S△BCM+S△ABC,∴S△ABN=S△BCM=3,∵A(1,0),B(﹣3,0),∴AB=4,∴S△ABN=![]() ×AB×n=
×AB×n=![]() ×4×n=2n=3,∴n=
×4×n=2n=3,∴n=![]() ,∵N在抛物线解析式为
,∵N在抛物线解析式为![]() 的图象上,∴
的图象上,∴![]() ,∴m1=
,∴m1=![]() ,m2=
,m2=![]() ,∴N(
,∴N(![]() ,
, ![]() )或N(
)或N(![]() ,
, ![]() );
);
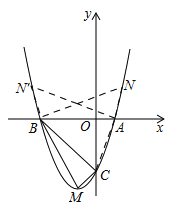
②如图2,点N在x轴下方的抛物线上,∵点C在对称轴的右侧,∴点N在对称轴右侧不存在,只有在对称轴的左侧,过点M作MN∥BC,交抛物线于点N,∵B(﹣3,0),C(0,﹣3),∴直线BC解析式为y=﹣x﹣3,设MN的解析式为y=﹣x+b,∵抛物线解析式为![]() ①,∴M(﹣1,﹣4),∴直线MN解析式为y=﹣x﹣5②,联立①②得:
①,∴M(﹣1,﹣4),∴直线MN解析式为y=﹣x﹣5②,联立①②得: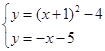 ,解得:
,解得: ![]() (舍),
(舍),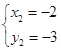 ,∴N(﹣2,﹣3).
,∴N(﹣2,﹣3).
综上所述:N(![]() ,
, ![]() )或N(
)或N(![]() ,
, ![]() )或N(﹣2,﹣3).
)或N(﹣2,﹣3).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2﹣4x+3=0的两根为x1 , x2 , 那么(1+x1)(1+x2)的值是
-
科目: 来源: 题型:
查看答案和解析>>【题目】周星驰的新春大片《美人鱼》创造了无数票房记录,从开始上映到3月6日9时止,票房累计达33亿元,33亿元用科学记数法表示为( )
A.33×108元
B.3.3×109元
C.3.3×1010元
D.0.33×1010元 -
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)(x+1)(x-2)=x+1; (2) x2-
 x=1
x=1(3)
 (4)
(4) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )

A. 20×(
 )4030 B. 20×(
)4030 B. 20×(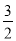 )4032 C. 20×(
)4032 C. 20×( )2016 D. 20×(
)2016 D. 20×( )2015
)2015 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.
其中说法正确的有_________(把你认为说法正确的序号都填上).

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家体育场“鸟巢”的建筑面积达258000m2 , 用科学记数法表示为( )
A.25.8×105
B.2.58×105
C.2.58×106
D.0.258×107
相关试题

