【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为Rt△ABC的斜边,四边形ABGM,APQC,BCDE均为正方形,四边形RFHN是长方形,若BC=3,AC=4,则图中空白部分的面积是______.

参考答案:
【答案】60
【解析】
根据勾股定理求出AB,求出△ACB≌△BOG≌△GHM,求出AC=OB=HG=4,BC=OG=MH=3,分别求出长方形FHNR,正方形BCDE,正方形ACQP,正方形ABGM的面积,即可求出答案.
解:如图,在Rt△ABC中,BC=3,AC=4,则根据勾股定理得到AB=![]() =5.
=5.

延长CB交FH于O,
∵四边形ABGM,APQC,BCDE均为正方形,
∴BG=AB=GM,∠ACB=∠ABG=∠F=∠H=∠MGB=90°,BC∥DE,
∴∠BOG=∠F=90°,
∴∠CAB+∠ABC=90°,∠ABC+∠GBO=180°-90°=90°,
∴∠CAB=∠GBO,
在△ACB和△BOG中,
 ,
,
∴△ACB≌△BOG(AAS),
∴AC=OB=4,OG=BC=3,
同理可证△MHG≌△GOB,
∴MH=OG=3,HG=OB=4,
∴FR=4+3+4=11,FH=3+3+4=10,
∴S空白=S长方形HFRN-S正方形BCDE-S正方形ACQP-S正方形ABGM
=11×10-3×3-4×4-5×5=60,
故答案为:60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年4月20日,我省芦山县发生7.0级强烈地震,造成大量的房屋损毁,急需大量帐篷.某企业接到任务,须在规定时间内生产一批帐篷.如果按原来的生产速度,每天生产120顶帐篷,那么在规定时间内只能完成任务的90%.为按时完成任务,该企业所有人员都支援到生产第一线,这样,每天能生产160顶帐篷,刚好提前一天完成任务.问规定时间是多少天?生产任务是多少顶帐篷?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在Rt△ABC中,∠C=90°,BC=1,AC=
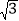 ,点D是斜边AB的中点,点E是边AC上一点,则DE+BE的最小值为( )
,点D是斜边AB的中点,点E是边AC上一点,则DE+BE的最小值为( )
A. 2
B.

C.
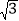
D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面四个整式中,不能表示图中阴影部分面积的是 ( )
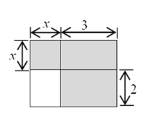
A.
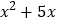 B.
B. 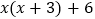 C.
C.  D.
D. 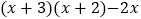
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;
②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线. 其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】宜宾是国家级历史文化名城,大观楼是标志性建筑之一(如图①).喜爱数学实践活动的小伟查资料得知:大观楼始建于明代(一说是唐代韦皋所建),后毁于兵火,乾隆乙酉年(1765年)重建,它是我国目前现存最高大、最古老的楼阁之一.小伟决定用自己所学习的知识测量大观楼的高度.如图②,他利用测角仪站在B处测得大观楼最高点P的仰角为45°,又前进了12米到达A处,在A处测得P的仰角为60°.请你帮助小伟算算大观楼的高度.(测角仪高度忽略不计,
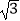 ≈1.7,结果保留整数).
≈1.7,结果保留整数).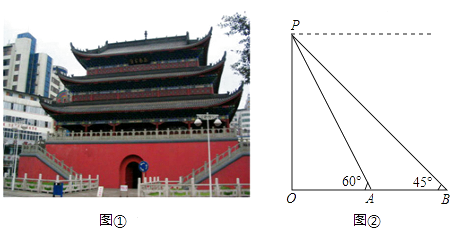
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x﹣1与反比例函数y=
 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m). 
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
相关试题

