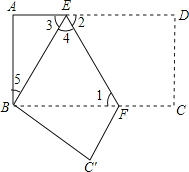
【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
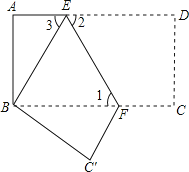
(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
参考答案:
【答案】(1)∠2=60°,∠3=60°(2)3![]()
【解析】
试题分析:(1)根据AD∥BC,∠1与∠2是内错角,因而就可以求得∠2,根据图形的折叠的定义,可以得到∠4=∠2,进而可以求得∠3的度数;
(2)已知AE=1,在Rt△ABE中,根据三角函数就可以求出AB、BE的长,BE=DE,则可以求出AD的长,就可以得到矩形的面积.
解:(1)∵AD∥BC,
∴∠2=∠1=60°;
又∵∠4=∠2=60°,
∴∠3=180°﹣60°﹣60°=60°.
(2)在直角△ABE中,由(1)知∠3=60°,
∴∠5=90°﹣60°=30°;
∴BE=2AE=2,
∴AB=![]() =
=![]() ;
;
∴AD=AE+DE=AE+BE=1+2=3,
∴长方形纸片ABCD的面积S为:ABAD=![]() ×3=3
×3=3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+kx+16是完全平方式,则k的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(-1,2),作点A关于y轴对称得到点A′,再将点A′向上平移2个单位,得到点A′′,则点A′′的坐标是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.
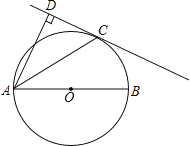
(1)求证:AC平分BAD;
(2)若AC=2
 ,CD=2,求⊙O的直径.
,CD=2,求⊙O的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A、B、C三点的坐标分别为(﹣6,7)、(﹣3,0)、(0,3).
(1)画出△ABC,并求△ABC的面积;
(2)在△ABC中,点C经过平移后的对应点为C′(5,4),将△ABC作同样的平移得到△A′B′C′, 画出平移后的△A′B′C′,并写出点A′,B′的坐标;
(3)已知点P(﹣3,m)为△ABC内一点,将点P向右平移4个单位后,再向下平移6个单位得到点Q(n,﹣3),则m= ,n= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有4个大小,质地都相同的乒乓球,球面上分别标有数字1,-2,3,-4,小明先从布袋中随机摸出一个球(不放回去),再从剩下的3个球中随机摸出第二个乒乓球.
(1)共有 种可能的结果.
(2)请用画树状图或列表的方法求两次摸出的乒乓球的数字之积为偶数的概率.
-
科目: 来源: 题型:
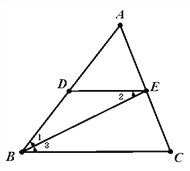
查看答案和解析>>【题目】如图所示,已知BE平分∠ABC,∠1=∠2,求证:∠AED=∠C.完善以下推理过程。
证明:∵BE平分∠ABC,∴∠1=∠3.( )
又∵∠1=∠2(已知),∴ = ( 等量代换),
∴ ∥ ( )
∴∠AED=∠C( )
相关试题

