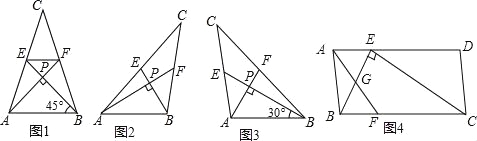
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4![]() 时,a= ,b= ;
时,a= ,b= ;
如图2,当∠PAB=30°,c=2时,a= ,b= ;
【归纳证明】
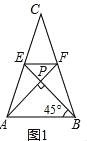
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
【拓展证明】
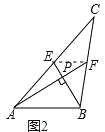
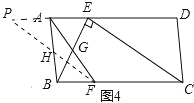
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
参考答案:
【答案】(1)4![]() ,4
,4![]() ;
;![]() ,
,![]() .(2)a2+b2=5c2,理由见解析.(3)4.
.(2)a2+b2=5c2,理由见解析.(3)4.
【解析】
试题分析:(1)①首先证明△APB,△PEF都是等腰直角三角形,求出PA、PB、PE、PF,再利用勾股定理即可解决问题.②连接EF,在RT△PAB,RT△PEF中,利用30°性质求出PA、PB、PE、PF,再利用勾股定理即可解决问题.(2)结论a2+b2=5c2.设MP=x,NP=y,则AP=2x,BP=2y,利用勾股定理分别求出a2、b2、c2即可解决问题.(3)取AB中点H,连接FH并且延长交DA的延长线于P点,首先证明△ABF是中垂三角形,利用(2)中结论列出方程即可解决问题.
试题解析:(1)解:如图1中,∵CE=AE,CF=BF,
∴EF∥AB,EF=![]() AB=2
AB=2![]() ,
,
∵tan∠PAB=1,
∴∠PAB=∠PBA=∠PEF=∠PFE=45°,
∴PF=PE=2,PB=PA=4,
∴AE=BF=![]() =2
=2![]() .
.
∴b=AC=2AE=4![]() ,a=BC=4
,a=BC=4![]() .
.
如图2中,连接EF,
,∵CE=AE,CF=BF,
∴EF∥AB,EF=![]() AB=1,
AB=1,
∵∠PAB=30°,
∴PB=1,PA=![]() ,
,
在RT△EFP中,∵∠EFP=∠PAB=30°,
∴PE=![]() ,PF=
,PF=![]() ,
,
∴AE=![]() =
=![]() ,BF=
,BF=![]() =
=![]() ,
,
∴a=BC=2BF=![]() ,b=AC=2AE=
,b=AC=2AE=![]() ,
,
(2)结论
证明:如图3中,连接EF.
∵AF、BE是中线,
∴EF∥AB,EF=![]() AB,
AB,
∴△FPE∽△APB,
∴![]() =
=![]() =
=![]() ,
,
设FP=x,EP=y,则AP=2x,BP=2y,
∴a2=BC2=4BF2=4(FP2+BP2)=4x2+16y2,
b2=AC2=4AE2=4(PE2+AP2)=4y2+16x2,
c2=AB2=AP2+BP2=4x2+4y2,
∴a2+b2=20x2+20y2=5(4x2+4y2)=5c2.
(3)解:如图4中,在△AGE和△FGB中,
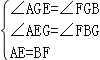 ,
,
∴△AGE≌△FGB,
∴BG=FG,取AB中点H,连接FH并且延长交DA的延长线于P点,
同理可证△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
即PE∥CF,PE=CF,
∴四边形CEPF是平行四边形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)可知AB2+AF2=5BF2,
∵AB=3,BF=![]() AD=
AD=![]() ,
,
∴9+AF2=5×(![]() )2,
)2,
∴AF=4.

-
科目: 来源: 题型:
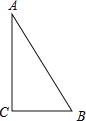
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的面积;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
(4)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列去括号正确的是( )
A.a+(b﹣c)=a+b+c
B.a﹣(b﹣c)=a﹣b﹣c
C.a﹣(b﹣c)=a﹣b+c
D.a+(b﹣c)=a﹣b+c -
科目: 来源: 题型:
查看答案和解析>>【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
 =1.732,
=1.732, =1.414)
=1.414)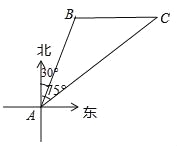
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b是方程x2﹣x﹣3=0的两个根,则代数式a3﹣a2+3b﹣2的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2 , 则S1+S2的值为( )

A. 16 B. 17 C. 18 D. 19
相关试题

