【题目】已知x1,x2是一元二次方程4kx2﹣4kx+k+2=0的两个实数根.是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=﹣![]() 成立?若存在,求出k的值;若不存在,请您说明理由.
成立?若存在,求出k的值;若不存在,请您说明理由.
参考答案:
【答案】(1)证明见解析;(2)不存在这样k的值,理由见解析.
【解析】分析:先利用一元二次方程的定义和根的判别式得到4k≠0,且△=(-4k) -4k(k+2)≥0,解得k<0,再利用根与系数的关系得到![]() +
+![]() =1,
=1, ![]()
![]() =
=![]() ,再利用(2
,再利用(2![]()
![]() )(
)(![]() -2
-2![]() )= -
)= -![]() 得到2(
得到2(![]() +
+![]() )29(
)29(![]()
![]() )=
)=![]() ,所以2×19
,所以2×19![]() =
=![]() 然后解得k=
然后解得k=![]() ,利用k<0可判定不存在k的值.
,利用k<0可判定不存在k的值.
本题解析:
(1) 不存在。
理由如下:
根据题意得4k≠0,且△=(4k)4k(k+2) ≥0,
∴k<0,
∵![]() ,
,![]() 是一元二次方程4kx4kx+k+2=0的两个实数根,
是一元二次方程4kx4kx+k+2=0的两个实数根,
∴![]() +x2=1,
+x2=1, ![]()
![]() =
=![]() ,
,
∵(2![]()
![]() )(
)( ![]() 2
2![]() )=
)=![]() ,
,
∴2(![]() +
+![]() )29(
)29(![]()
![]() )=
)=![]() ,
,
∴2×19![]() =
=![]() ,解得k=
,解得k=![]() ,
,
而k<0,
∴不存在k的值,使(2![]()
![]() )(
)( ![]() 2
2![]() )=
)=![]() 成立。
成立。
-
科目: 来源: 题型:
查看答案和解析>>【题目】将连续的偶数2,4,6,8……,排成如下表:

(1)十字框中的五个数的和与中间的数16有什么关系?
(2)设中间的数为x,用代数式表示十字框中的五个数的和,
(3)若将十字框上下左右移动,可框住另外的五个数,其它五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3﹣(﹣5)+7=;计算﹣2﹣|﹣6|的结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程(k-1)x2+2kx+2=0
(1)(4分)求证:无论k为何值,方程总有实数根。
(2)(5分)设x1,x2是方程(k-1)x2+2kx+2=0的两个根,记S=
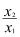 +
+ + x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。
+ x1+x2,S的值能为2吗?若能,求出此时k的值。若不能,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 有一个角是直角的四边形是矩形
B. 矩形的对角线相等
C. 矩形的对角线互相平分
D. 有一个角是直角的平行四边形是矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是( )
A.a>2
B.a<2
C.a<2且a≠l
D.a<﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:2x﹣y=5,求﹣2(y﹣2x)2+3y﹣6x的值.
相关试题

