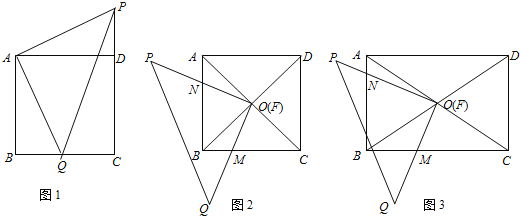
【题目】(1)正方形ABCD与等腰直角三角形PAQ如图1所示重叠在一起,其中∠PAQ=90°,点Q在BC上,连接PD,△ADP与△ABQ全等吗?请说明理由.
(2)如图2,O为正方形ABCD对角线的交点,将一直角三角板FPQ的直角顶点F与点O重合转动三角板使两直角边始终与BC、AB相交于点M、N,使探索OM与ON的数量关系,并说明理由.
(3)如图3,将(2)中的“正方形”改成“长方形”,其它的条件不变,且AB=4,AD=6,FM=x,FN=y,试求y与x之间的函数关系式.
参考答案:
【答案】(1)△ADP≌△ABQ,理由见解析;
(2)AC⊥BD,理由见解析;
(3)y与x之间的函数关系式为: ![]() .
.
【解析】试题分析:(1)根据正方形的性质和等腰直角三角形的性质就可以求得△ADP与△ABQ全等;
(2)根据正方形的性质和等腰直角三角形的性质就可以得△ANO≌△BMO,从而得出ON=OM;
(3)过点O作OE⊥AB于E,OH⊥BC于H,由条件求出OE、OH的值,再通过证明△OEN∽△OHM,利用相似三角形的性质就可以求出结论.
试题解析:(1)△ADP≌△ABQ.
理由:如图1,∵四边形ABCD是正方形,
∴AB=AD,∠B=∠ADP=∠BAD=90°
∵△PAQ是等腰直角三角形,
∴AQ=AP.
∵∠PAQ=90°,
∴∠BAD=∠PAQ,
∴∠BAD-∠QAD=∠PAQ-∠QAD,
∴∠BAQ=∠PAD.
∵在△ADP和△ABQ中,
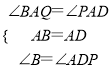
∴△ADP≌△ABQ(ASA);
(2)OM=ON.
理由:如图2,∵四边形ABCD是正方形,
∴AO=BO,∠AOB=90°,∠OAB=∠OBC=45°.
∴∠AOB=∠POQ,
∴∠AOB-∠NOB=∠POQ-∠NOB,
∴∠AON=∠BOM
∵在△AON和△BOM中,
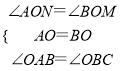 ,
,
∴△AON≌△BOM(ASA)
∴OM=ON;
(3)如图4,
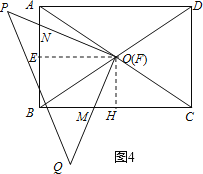
过点O作OE⊥AB于E,OH⊥BC于H,
∴∠OEN=∠OHM=90°,OE=![]() AD,OH=
AD,OH=![]() AB.
AB.
∵AB=4,AD=6,
∴OE=3,OH=2.
∵∠ABC=90°,
∴四边形EBHO是矩形,
∴∠EOH=90°,
∴∠EOH=∠POQ,
∴∠EOH-∠EOM=∠POQ-∠EOM,
∴∠EON=∠HOM.
∴△OEN∽△OHM,
∴![]() ,
,
即![]()
∴y= ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次数学课外活动中,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向,办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(结果精确到0.1米).(供选用的数据:
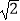 ≈1.414,
≈1.414,  ≈1.732)
≈1.732)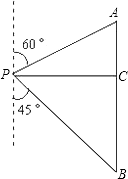
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察、思考、解答: (
 ﹣1)2=(
﹣1)2=(  )2﹣2×1×
)2﹣2×1×  +12=2﹣2
+12=2﹣2  +1=3﹣2
+1=3﹣2 
反之3﹣2 =2﹣2
=2﹣2  +1=(
+1=(  ﹣1)2
﹣1)2
∴3﹣2 =(
=(  ﹣1)2
﹣1)2
∴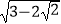 =
=  ﹣1
﹣1
(1)仿上例,化简: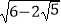 ;
;
(2)若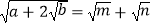 ,则m、n与a、b的关系是什么?并说明理由;
,则m、n与a、b的关系是什么?并说明理由;
(3)已知x=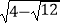 ,求(
,求( 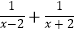 )
) 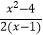 的值(结果保留根号)
的值(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
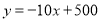 .
.(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简(2x)2的结果是( )
A.x4
B.2x2
C.4x2
D.4x -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.

相关试题

