【题目】如果抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 上,同时,抛物线
上,同时,抛物线![]() 的顶点在抛物线
的顶点在抛物线![]() 上,那么,我们称抛物线
上,那么,我们称抛物线![]() 与
与![]() 关联.
关联.
(1)已知抛物线![]() ,判断下列抛物线:①
,判断下列抛物线:①![]() ;②
;②![]()
![]() 与已知抛物线是否关联,并说明理由;
与已知抛物线是否关联,并说明理由;
(2)已知抛物线![]() :
: ![]() ,点P的坐标为
,点P的坐标为![]() ,将抛物线绕点
,将抛物线绕点![]() 旋转180°得到抛物线
旋转180°得到抛物线![]() (此处我们称点P为旋转点),若抛物线
(此处我们称点P为旋转点),若抛物线![]() 与
与![]() 关联,求抛物线
关联,求抛物线![]() 的解析式;
的解析式;
(3)在(2)的条件下,已知点![]() 是抛物线
是抛物线![]() 上的一点,求以点A为顶点并与抛物线
上的一点,求以点A为顶点并与抛物线![]() 相关联的抛物线
相关联的抛物线![]() 的解析式,并判断此时抛物线
的解析式,并判断此时抛物线![]() 能否由抛物线
能否由抛物线![]() 旋转得来?若能,请求出旋转点坐标;若不能,请说明你的理由;
旋转得来?若能,请求出旋转点坐标;若不能,请说明你的理由;
(4)由上述结论猜想:若两抛物线![]() 相关联,则它们的二次式项系数(分别记为
相关联,则它们的二次式项系数(分别记为![]() )应满足数量关系: .
)应满足数量关系: .
参考公式(中点坐标公式):若点![]() ,则线段AB的中点坐标为
,则线段AB的中点坐标为![]() .
.
参考答案:
【答案】(1)抛物线①与已知抛物线相关联,而抛物线②不与已知抛物线相关联,理由见解析;(2)抛物线![]() :
: ![]() 或
或![]() ;(3)旋转点
;(3)旋转点![]() ;(4)
;(4)![]() .
.
【解析】试题分析:(1)首先求出抛物线①、②的顶点坐标,然后根据定义的抛物线关联条件即可进行判断.
(2)先求出抛物线C1的顶点坐标,设C2顶点为(x,y),根据旋转可知抛物线C2的顶点与C1的顶点关于点P(t,-1)对称,从而可用含t的代数式表示C2的顶点坐标,然后根据定义代入C1的解析式,确定出C2的顶点,从而可求出C2的解析式;
(3)根据题意求出A点坐标,从而可利用顶点式来确定C2的解析式,从而可确定出旋转点的坐标;
(4)根据定义若关联,则二次项系数互为相反数,从而可得.
试题解析:(1)已知抛物线![]() ,顶点坐标为
,顶点坐标为![]() ,
,
抛物线①![]() ,顶点坐标为
,顶点坐标为![]() ,
,
抛物线②![]() ,顶点坐标为
,顶点坐标为![]() ,
,
很明显点![]() 在抛物线①
在抛物线①![]() 上,且点
上,且点![]() 也在已知抛物线
也在已知抛物线
![]() 上,而点
上,而点![]() 并不在已知抛物线
并不在已知抛物线![]() 上,
上,
故抛物线①与已知抛物线相关联,而抛物线②不与已知抛物线相关联;
(2)抛物线![]() :
: ![]() ,顶点坐标为
,顶点坐标为![]() ,
,
设抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,根据中点坐标公式:
,根据中点坐标公式: 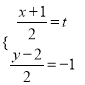 ,
,
解得: ![]() .将
.将![]() 代入抛物线
代入抛物线![]() ,
,
即: ![]() ,解得:t=0或t=2,
,解得:t=0或t=2,
即抛物线![]() 的顶点坐标为
的顶点坐标为![]() 或
或![]() .
.
又抛物线![]() 与抛物线
与抛物线![]() 开口大小相同,但方向相反,
开口大小相同,但方向相反,
∴抛物线![]() :
: ![]() 或
或![]() ,
,
即抛物线![]() :
: ![]() 或
或![]() ;
;
(3)将![]() 代入抛物线
代入抛物线![]() ,得:
,得: ![]() ,∴
,∴![]() .
.
设抛物线![]() :
: ![]() ,将抛物线
,将抛物线![]() 的顶点
的顶点![]() 代入,
代入,
解得: ![]() .此时抛物线
.此时抛物线![]() :
: ![]() ,即
,即![]() .
.
∵两抛物线开口大小相同,但方向相反,∴抛物线![]() 能否由抛物线
能否由抛物线![]() 旋转得来,
旋转得来,
旋转点为两顶点![]() 与
与![]() 的中点,即
的中点,即![]() .
.
(4)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球上的陆地面积约为149000000平方千米,这个数字用科学记数法表示应为( )
A.0.149×106
B.1.49×107
C.1.49×108
D.14.9×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1 , B2 , B3 , …,则B2014的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在函数y=kx(k>0)的图象上有三点A1(x1,y1),A2(x2,y2),A3(x3,y3),已知x1<x2<0<x3,则下列各式中正确的是( )
A. y1<0<y3 B. y3<0<y1 C. y2<y1<y3 D. y3<y1<y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一次函数y=3x﹣1的图象沿y轴向上平移3个单位后,得到的图象对应的函数关系式为__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(长春中考)在“世界家庭日”前夕,某校团委随机抽取n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查.问卷中的家庭活动方式包括:
A.在家里聚餐 B.去影院看电影
C.到公园游玩 D.进行其他活动
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式.该校团委收回全部问卷后,将收集到的数据整理并绘制成如下的统计图.根据统计图提供的信息,解答下列问题:
n名学生喜欢的家庭活动方式的人数条形统计图
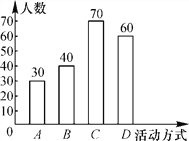
(1)求n的值;
(2)四种方式中最受学生喜欢的方式为C(用A,B,C,D作答);选择该种方式的学生人数占被调查的学生人数的百分比为______;
(3)根据统计结果,估计该校1 800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂2014年缴税20万元,2016年缴税24万元,这这两年该工厂缴税的年平均增长率为x,根据题意,可得方程为 .
相关试题

