搜索
【题目】如图，已知△ABC是等边三角形，D为边AC的中点，AE⊥EC，BD=EC，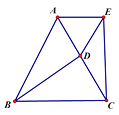
（1）说明△BCD与△CAE全等的理由
（2）请判断△ADE的形状，并说明理由．
参考答案：
【答案】
（1）解：∵△ABC是等边三角形
∴AB=BC=AC，∠ACB=60°
又∵D为AC中点
∴BD⊥AC，AD=CD
又∵AE⊥EC
∴∠BDC=∠AEC=90°
又∵BD=CE
∴Rt△BDC≌Rt△CEA
（2）解：∵Rt△BDC≌Rt△CEA
∴∠EAC=∠ACB=60°，AE=CD
又∵D为边AC的中点，
∴AD=CD，
∴AD=AE
∴△ADE是等边三角形．
【解析】（1）利用等边三角形的性质和“HL"可判定全等；（2）由（1）的结论和已知，利用”有一个角为60度的等腰三角形是等边三角形“证出结论.
-
科目： 来源： 题型：
查看答案和解析>>【题目】若方程2x=8和方程ax+2x=4的解相同，则a的值为（ ）
A.1
B.﹣1
C.±1
D.0 -
科目： 来源： 题型：
查看答案和解析>>【题目】不解方程，判断方程2x2﹣3x+1=0的根的情况是（ ）
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根 -
科目： 来源： 题型：
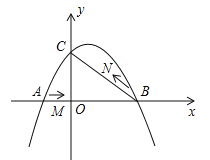
查看答案和解析>>【题目】如图，在平面直角坐标系中，抛物线
（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B坐标为（4，0），抛物线的对称轴方程为x=1．（1）求抛物线的解析式；
（2）点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN的面积为S，点M运动时间为t，试求S与t的函数关系，并求S的最大值；
（3）在点M运动过程中，是否存在某一时刻t，使△MBN为直角三角形？若存在，求出t值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]=2，（2.3）=3，[2.3）=2．则下列说法正确的是 ．（写出所有正确说法的序号）
①当x=1.7时，[x]+（x）+[x）=6；
②当x=﹣2.1时，[x]+（x）+[x）=﹣7；
③方程4[x]+3（x）+[x）=11的解为1＜x＜1.5；
④当﹣1＜x＜1时，函数y=[x]+（x）+x的图象与正比例函数y=4x的图象有两个交点．
-
科目： 来源： 题型：
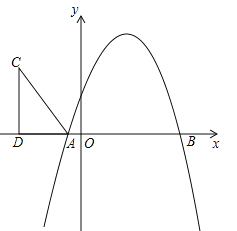
查看答案和解析>>【题目】如图，抛物线y=﹣x2+bx+c与x轴分别交于A（﹣1，0），B（5，0）两点．
（1）求抛物线的解析式；
（2）在第二象限内取一点C，作CD垂直X轴于点D，链接AC，且AD=5，CD=8，将Rt△ACD沿x轴向右平移m个单位，当点C落在抛物线上时，求m的值；
（3）在（2）的条件下，当点C第一次落在抛物线上记为点E，点P是抛物线对称轴上一点．试探究：在抛物线上是否存在点Q，使以点B、E、P、Q为顶点的四边形是平行四边形？若存在，请出点Q的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“节能环保，低碳生活”是我们倡导的一种生活方式．某家电商场计划用12万元购进节能型电视机、洗衣机和空调共40台．三种家电的进价及售价如表所示：
种类
进价（元/台）
售价（元/台）
电视机
5000
5480
洗衣机
2000
2280
空 调
2500
2800
（1）在不超出现有资金的前提下，若购进电视机的数量和洗衣机的数量相同，空调的数量不超过电视机的数量的三倍．请问商场有哪几种进货方案？
（2）在“2016年消费促进月”促销活动期间，商家针对这三种节能型产品推出“现金每购1000元送50元家电消费券一张、多买多送”的活动．在（1）的条件下，若三种电器在活动期间全部售出，商家预计最多送出消费券多少张？
相关试题
