【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°。
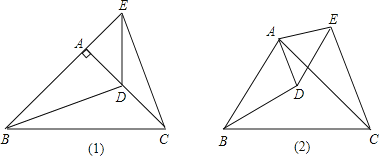
①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?写出你猜想的结论,并说明理由;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由。
参考答案:
【答案】①BD=CE,BD⊥CE,理由见解析;②BD=CE,BD⊥CE,理由见解析.
【解析】
试题分析:①BD=CE,BD⊥CE.根据全等三角形的判定定理SAS推知△ABD≌△ACE,然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA;然后在△ABD和△CDF中,由三角形内角和定理可以求得∠CFD=90°,即BD⊥CF;②BD=CE,BD⊥CE.根据全等三角形的判定定理SAS推知△ABD≌△ACE,然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA;作辅助线(延长BD交AC于F,交CE于H)BH构建对顶角∠ABF=∠HCF,再根据三角形内角和定理证得∠BHC=90°;
试题解析:解:①结论:BD=CE,BD⊥CE;理由如下:
在△ABD与△ACE中,
AB=AC,AD=AE,∠BAC=∠DAE=90°
∴△ABD≌△ACE(SAS)
∴BD=CE
如图(1),延长BD交CE于F,
∠ABD=∠ACE,∠ADB=∠CDF=∠EAC,
∴BD⊥CE
②结论:BD=CE,BD⊥CE
理由如下:∵∠BAC=∠DAE=90°
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE
在△ABD与△ACE中,
∵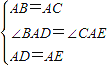
∴△ABD≌△ACE(SAS)
∴BD=CE
如图(2)延长BD交AC于F,交CE于H.
在△ABF与△HCF中,
∵∠ABF=∠HCF,∠AFB=∠HFC
∴∠CHF=∠BAF=90°
∴BD⊥CE

-
科目: 来源: 题型:
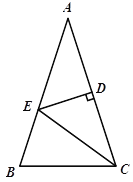
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC.
(1)求∠ECD的度数;
(2)若CE=12,求BC长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是
A.某市八年级学生的肺活量 B.从中抽取的500名学生的肺活量
C.从中抽取的500名学生 D.500
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了考察某市3万名中考学生的数学考试成绩,从中抽取了10本试卷,每本30份,在这个问题中,样本容量是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解学生家长对孩子用手机的态度问题,随机抽取了100名家长进行问卷调查,每位学生家长只有一份问卷,且每份问卷仅表明一种态度(这100名家长的问卷真实有效),将这100份问卷进行回收整理后,绘制了如下两幅不完整的统计图.

(1)“从来不管”的问卷有 份,在扇形图中“严加干涉”的问卷对应的圆心角为 .
(2)请把条形图补充完整.
(3)若该校共有学生2000名,请估计该校对手机问题“严加干涉”的家长有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:4x﹣6=2(3x﹣1)
相关试题

