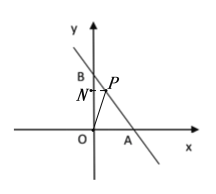
【题目】如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
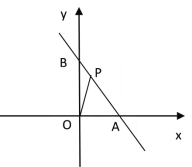
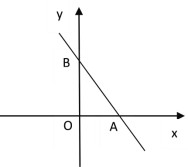
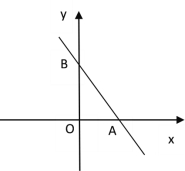
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
参考答案:
【答案】(1)6;(2)S=3m,0<m<4;(3)y=3x或y= -3x
【解析】
(1)根据点坐标可得△POA的底和高,根据三角形面积公式计算;(2)根据点坐标可得△POB的底和高,根据三角形面积公式列出S与m的解析式;(3)分别讨论当P在第二、第一、第四象限内,根据题意列出等式求P点坐标,确定直线OP解析式.
解:(1)如图,过P作PM⊥x轴,垂足为M,
∵A(4,0),P(2,3),
∴S△POA=![]() =
=![]() .
.
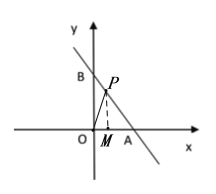
(2)如图,过P作PN⊥y轴,垂足为N,
∵B(0,6),P(m,n),
∴S =![]() =
=![]() .
.
∵P在线段AB上(不与点A、B重合)
∴0<m<4
∴S关于m的函数解析式为S=3m,0<m<4.
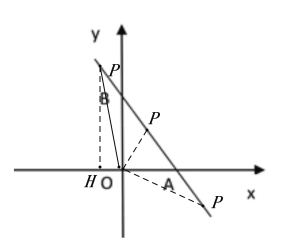
(3)如图,设直线AB的解析式为y=kx+b,将A(4,0),B(0,6)代入,
![]() ,
,
解得,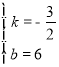 ,
,
∴直线AB的解析式为![]() ,
,
∴P(m, ![]() ).
).
∵S△BOP:S△POA=1:2,∴S△POA=2 S△BOP
①当m≤0,即点P在第二象限时,
根据题意得,![]()
解得,m= -4,
∴P(-4,12),
设直线OP解析式为y=ax,将P点代入,
-4a=12,
解得,a= -3,
∴直线OP解析式为y= -3x;
②当0<m≤4,即点P在第一象限时,
根据题意得,![]()
解得,m=![]() ,
,
∴P(![]() ,4),
,4),
设直线OP解析式为y=ax,将P点代入,
![]() a=4,
a=4,
解得,a= 3,
∴直线OP解析式为y= 3x;
③当m>4,即点P在第四象限时,
根据题意得,![]()
解得,m= -4(不符合题意,舍去) .
综上所述,直线OP的解析式为:y=3x或y= -3x
-
科目: 来源: 题型:
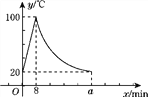
查看答案和解析>>【题目】教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10 ℃,待加热到100 ℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20 ℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40 ℃的开水,则他需要在什么时间段内接水?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家______ 千米,张强从家到体育场用了______ 分钟;
(2)体育场离文具店______ 千米;
(3)张强在文具店逗留了______ 分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,AC平分∠BAD,CE⊥AB于E,∠ADC+∠CBE=180°,求证:2AE=AB+AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )
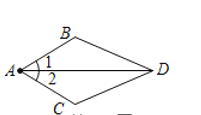
A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=
 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=
 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
相关试题

