【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
参考答案:
【答案】
(1)
解:作BD⊥AC于点D,如图所示:
由题意可知:AB=30×1=30海里,∠BAC=30°,∠BCA=45°,
在Rt△ABD中,
∵AB=30海里,∠BAC=30°,
∴BD=15海里,AD=ABcos30°=15 ![]() 海里,
海里,
在Rt△BCD中,
∵BD=15海里,∠BCD=45°,
∴CD=15海里,BC=15 ![]() 海里,
海里,
∴AC=AD+CD=15 ![]() +15海里,
+15海里,
即A、C间的距离为(15 ![]() +15)海里.
+15)海里.

(2)
解:∵AC=15 ![]() +15(海里),
+15(海里),
轮船乙从A到C的时间为 ![]() =
= ![]() +1,
+1,
由B到C的时间为 ![]() +1﹣1=
+1﹣1= ![]() ,
,
∵BC=15 ![]() 海里,
海里,
∴轮船甲从B到C的速度为 ![]() =5
=5 ![]() (海里/小时).
(海里/小时).
【解析】(1)根据题意画出图形,再根据平行线的性质及直角三角形的性质解答即可.(2)根据甲乙两轮船从港口A至港口C所用的时间相同,可以求出甲轮船从B到C所用的时间,又知BC间的距离,继而求出甲轮船后来的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)3ab2(﹣
 a2b)2abc;
a2b)2abc;(2)(﹣
 x2y)3(﹣3xy2);
x2y)3(﹣3xy2);(3)(﹣3xy2)3(
 x3y);
x3y);(4)(x2+3x)﹣2(4x﹣x2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
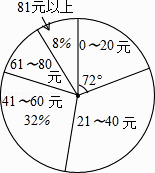
捐款
人数
0~20元
21~40元
41~60元
61~80元
6
81元以上
4
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣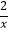 的图象上的概率.
的图象上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.
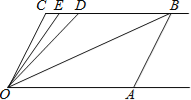
(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,AE是BC边上的高,∠ADB=106°,∠C=56°,求∠DAE和∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8;乙:9,6,10,8,7;
 将下表填写完整:
将下表填写完整:平均数
中位数
方差
甲
______
8
______
乙
8
______
2
 根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么? 若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______
若乙再射击一次,命中8环,则乙这六次射击成绩的方差会______ 填“变大”或“变小”或“不变”
填“变大”或“变小”或“不变”
相关试题

