【题目】请在横线上填写合适的内容,完成下面的证明:
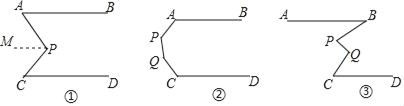
(1)如图①如果AB∥CD,求证:∠APC=∠A+∠C.
证明:过P作PM∥AB,
所以∠A=∠APM,( )
因为PM∥AB,AB∥CD(已知)
所以PM∥CD( )
所以∠C= ( )
因为∠APC=∠APM+∠CPM
所以∠APC=∠A+∠C( )
(2)如图②,AB∥CD,根据上面的推理方法,直接写出∠A+∠P+∠Q+∠C= .
(3)如图③,AB∥CD,若∠ABP=x,∠BPQ=y,∠PQC=z,∠QCD=m,则m= (用x、y、z表示)
参考答案:
【答案】(1)两直线平行,内错角相等;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;∠CPM;两直线平行,内错角相等;等量代换;(2)540°;(3)x﹣y+z.
【解析】
(1)根据平行线的性质和判定填
(2)过点P作PE∥AB,过点Q作QF∥AB,根据平行线的性质可求.
(3)过点P作PE∥AB,过点Q作QF∥AB,根据平行线的性质可求.
(1)过P作PM∥AB,
所以∠A=∠APM,(两直线平行,内错角相等),
因为PM∥AB,AB∥CD(已知),
所以PM∥CD(如果两条直线都与第三条直线平行,那么这两条直线也互相平行),
所以∠C=∠CPM(两直线平行,内错角相等),
因为∠APC=∠APM+∠CPM,
所以∠APC=∠A+∠C(等量代换),
故答案为:两直线平行,内错角相等;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;∠CPM;两直线平行,内错角相等;等量代换.
(2)如图过点P作PE∥AB,过点Q作QF∥AB
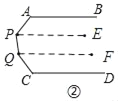
∵AB∥DC,PE∥AB,QF∥AB,
∴AB∥PE∥QF∥CD,
∴∠A+∠APE=180°,
∠EPQ+∠PQF=180°,
∠FQC+∠QCD=180°,
∴∠A+∠APQ+∠PQC+∠C=540°,
故答案为:540°;
(3)如图:过点P作PE∥AB,过点Q作QF∥AB,
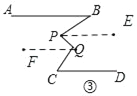
∵AB∥DC,PE∥AB,QF∥AB,
∴AB∥PE∥QF∥CD,
∴∠B=∠BPE,∠BPE=∠PQF,∠FQC=∠C,
∴∠B+∠PQC=∠C+∠BPQ,
即x+z=m+y,
m=x﹣y+z,
故答案为x﹣y+z.
-
科目: 来源: 题型:
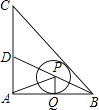
查看答案和解析>>【题目】如图,在等腰三角形ABC中,∠BAC=90°,AB=AC=1,BD平方∠ABC,点P在BD上,⊙P切AB于点Q,则AP+PQ的最小值等于 .
-
科目: 来源: 题型:
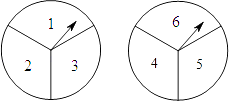
查看答案和解析>>【题目】为了纪念中国共产主义青年团成立90周年,某校初三(1)、(2)班团支部组织了一次联欢会,小乐为活动设计了一个游戏:把两个可以自由转动的转盘各等分成三个扇形,分别标上1,2,3和4,5,6,每班级各派一名选手参加,每人同时转动两个转盘各一次(指针落在等分线上重转),转盘停止后,指针指向的数字之和为偶数时(1)班获胜,数字之和为奇数时(2)班获胜,小乐设计的游戏规则公平吗?请用树状图或列表分析说明,若认为不公平,请修改规则使游戏变得公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.

-
科目: 来源: 题型:
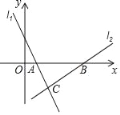
查看答案和解析>>【题目】如图,直线l1的函数表达式为y=﹣2x+2,且与x轴交于点A,直线l2经过点B(5,0)且与l1交于点C,已知点C的横坐标是2.
(1)求点A和点C的坐标;
(2)若在直线l2上存在异于点C的另一点M,使得△ABM与△ABC的面积相等,试求点M的坐标.
(3)在y轴上求点P的坐标,使得PA+PC最小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.
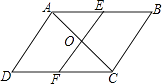
(1)求证:AE=CF;
(2)当EF⊥AC时,连接AF,CE,试判断四边形AFCE是怎样的四边形?并证明你的结论. -
科目: 来源: 题型:
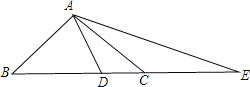
查看答案和解析>>【题目】(1)如图,在在△ABC中,已知∠BAC=900,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,CE=CA,求∠DAE的度数;
(2)如果把(1)中的“AB=AC”条件去掉,其余条件不变,那么∠DAE的度数改变吗?为什么?
(3)如果把(1)中的“∠BAC=900”改成“∠BAC>900”其余条件不变,试探究∠DAE与∠BAC的数量关系式,试证明.
相关试题

