Question

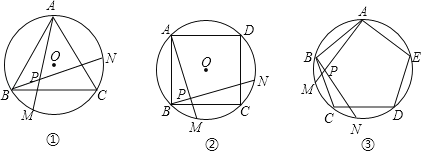
【题目】如图①、②、③，正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形，点M、N分别从点B、C开始，以相同的速度在⊙O上逆时针运动．

（1）求图①中∠APN的度数（写出解题过程）；

（2）写出图②中∠APN的度数和图③中∠APN的度数；

（3）试探索∠APN的度数与正多边形边数n的关系（直接写答案）

Answer 1

【答案】（1）∠APN=∠ABC=60°；（2）图2中，∠APN=∠ABC=90°；图3中，∠APN=∠ABC=108°；（3）∠APN=．

【解析】

试题分析：（1）由△ABC为等边三角形可知∠ABC=60°，再由等速运动可得到∠ABP=∠NBC，再利用外角的性质可得∠APN=∠ABP+∠BAP，代换可得到∠APN=∠ABC，可求得∠APN的度数；

（2）和（1）同理可得到∠APN的度数和∠ABC的度数相等，图③中∠APN的度数和∠ABC的度数相等；

（3）结合（1）（2）可得到∠APN的度数等于多边形的内角的度数，可得到结论．

解：（1）∠APN=60°．

∵∠APN=∠ABP+∠BAP，

且点M、N以相同的速度中⊙O上逆时针运动，

∴=，

∴∠ABP=∠NBC，

∴∠APN=∠ABP+∠NBC，

即∠APN=∠ABC=60°；

（2）同理：图2中，∠APN=∠ABC=90°；图3中，∠APN=∠ABC=108°；

（3）由（1）（2）可知∠APN的度数等于多边形的内角的度数，

当正多边形为n边形时，其内角和为（n﹣2）180°，

所以每个内角的度数为，

所以∠APN=．