【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

参考答案:
【答案】(1)足球飞行的时间是![]() s时,足球离地面最高,最大高度是4.5m;(2)能.
s时,足球离地面最高,最大高度是4.5m;(2)能.
【解析】试题分析:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),于是得到![]() ,求得抛物线的解析式为:y=﹣
,求得抛物线的解析式为:y=﹣![]() t2+5t+
t2+5t+![]() ,当t=
,当t=![]() 时,y最大=4.5;
时,y最大=4.5;
(2)把x=28代入x=10t得t=2.8,当t=2.8时,y=﹣![]() ×2.82+5×2.8+
×2.82+5×2.8+![]() =2.25<2.44,于是得到他能将球直接射入球门.
=2.25<2.44,于是得到他能将球直接射入球门.
解:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),
∴![]() ,
,
解得: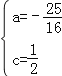 ,
,
∴抛物线的解析式为:y=﹣![]() t2+5t+
t2+5t+![]() ,
,
∴当t=![]() 时,y最大=4.5;
时,y最大=4.5;
(2)把x=28代入x=10t得t=2.8,
∴当t=2.8时,y=﹣![]() ×2.82+5×2.8+
×2.82+5×2.8+![]() =2.25<2.44,
=2.25<2.44,
∴他能将球直接射入球门.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点.现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.如图,若该抛物线经过原点O,且a=-
 .
.(1)求点D的坐标及该抛物线的解析式;
(2)连结CD.问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某民俗旅游村为接待游客住宿需要,开设了有100张床位的旅馆.当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A. 140元 B. 150元 C. 160元 D. 180元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=
 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2+ax+9=(x+3)2,那么a的值为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=(m2-3m+2)x|m|-3是反比例函数,则m的值是( )
A.1
B.-2
C.±2
D.2
相关试题

