搜索
【题目】关于二次函数
的图象与性质，下列结论错误的是 （ ）
A. 当x=3时，函数有最大值-2
B. 当x＞3时，y随x的增大而减小
C. 抛物线可由 
经过平移得到
D. 该函数的图象与x轴有两个交点
参考答案：
【答案】D
【解析】
根据二次函数的开口方向及二次函数最值得求法，可对A作出判断；根据二次函数的增减性，可对B作出判断；根据二次函数平移规律，可对C作出判断；根据二次函数与x轴的交点情况即b2-4ac的值的大小，可对D作出判断，从而可得出答案.
解：A、当 x=3时，函数有最大值 
，不符合题意；
B、当x＞3时，y随x的增大而减小，不符合题意；
C、抛物线可由
经过平移得到，不符合题意；
D、该函数的图象与x轴有没有交点，符合题意；
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等边三角形的顶点A（1，1）、B（3，1），规定把等边△ABC“先沿x轴翻折，再向左平移1个单位”为一次变换，如果这样连续经过2018次变换后，等边△ABC的顶点C的坐标为_____．
-
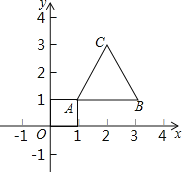
科目： 来源： 题型：
查看答案和解析>>【题目】在如图的方格中，每个小正方形的边长都为1，△ABC的顶点均在格点上．在建立平面直角坐标系后，点B的坐标为（﹣1，2）．
（1）把△ABC向下平移8个单位后得到对应的△A1B1C1，画出△A1B1C1；
（2）画出与△A1B1C1关于y轴对称的△A2B2C2；
（3）若点P（a，b）是△ABC边上任意一点，P2是△A2B2C2边上与P对应的点，写出P2的坐标为 ；
（4）试在y轴上找一点Q(在图中标出来)，使得点Q到B2、C2两点的距离之和最小，并求出QB2+QC2的最小值．
-
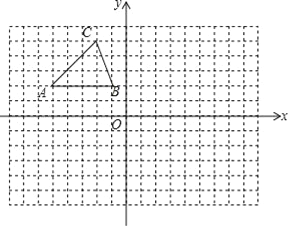
科目： 来源： 题型：
查看答案和解析>>【题目】设函数
（
为常数），下列说法正确的是（ ）．A. 对任意实数
，函数与
轴都没有交点B. 存在实数
，满足当
时，函数
的值都随
的增大而减小C.
取不同的值时，二次函数
的顶点始终在同一条直线上D. 对任意实数
，抛物线
都必定经过唯一定点 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，长方形OABC的边OC=2，将过点B的直线y=x﹣3与x轴交于点E．
（1）求点B的坐标；
（2）连结CE，求线段CE的长；
（3）若点P在线段CB上且OP=
，求P点坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，O是坐标原点，菱形OABC的顶点A（3，4），C在x轴的负半轴，抛物线y=﹣
（x﹣2）2+k过点A．（1）求k的值；
（2）若把抛物线y=﹣
（x﹣2）2+k沿x轴向左平移m个单位长度，使得平移后的抛物线经过菱形OABC的顶点C．试判断点B是否落在平移后的抛物线上，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知正比例函数y＝kx经过点A，点A在第四象限，过点A作AH⊥x轴，垂足为点H，点A的横坐标为3，且△AOH的面积为3．
（1）求正比例函数的表达式；
（2）在x轴上能否找到一点M，使△AOM是等腰三角形？若存在，求点M的坐标；若不存在，请说明理由．
相关试题
