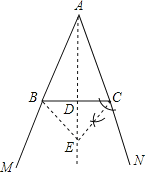
【题目】如图所示,点B和点C分别为∠MAN两边上的点,AB=AC.
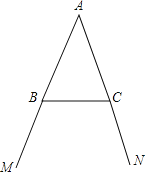
(1)按下列语句画出图形:
①AD⊥BC,垂足为D;
②∠BCN的平分线CE与AD的延长线交于点E;
③连接BE.
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形: ≌ , ≌ ;并选择其中的一对全等三角形,予以证明.
参考答案:
【答案】(1)见解析;(2)△BDE≌△CDE(SAS).见解析
【解析】
试题分析:(1)①从A作AD⊥BC,垂足为D,D在线段BC上;
②作∠BCN的平分线CE与AD的延长线交于点E,E在线段AD的延长线上;
③连接BE就是过B、E两点画线段;
(2)还有△ABE≌△ACE;△BDE≌△CDE.其中证明△ABE≌△ACE的条件有AB=AC、∠BAE=∠CAE、AE公共,由此即可证明;证明△BDE≌△CDE的全等条件有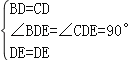 ,由此即可证明结论.
,由此即可证明结论.
解:(1)①②③,如图所示:
(2)△ABE≌△ACE,△BDE≌△CDE.
(3)选择△ABE≌△ACE进行证明.
∵AB=AC,AD⊥BC,
∴∠BAE=∠CAE,
在△ABE和△ACE中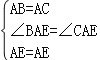
∴△ABE≌△ACE(SAS);
选择△BDE≌△CDE进行证明.
∵AB=AC,AD⊥BC,
∴BD=CD,
在△BDE和△CDE中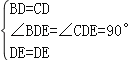 ,
,
∴△BDE≌△CDE(SAS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】张朋将连续10天引体向上的测试成绩(单位:个)记录如下:16,18,18,16,19,19,18,21,18,21.则这组数据的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=
 ∠ABC.
∠ABC.
(1)如图1,以点B为旋转中心,将△EBC按顺时针方向旋转,得到△E′BA(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;
(2)如图2,若∠ABC=90°,AD=4,EC=2,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛,对这两名运动员进行了10次测试,经过数据分析,甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024(s2),乙的方差为0.008(s2),则这10次测试成绩比较稳定的是 运动员.(填“甲”或“乙”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校女子排球队队员的年龄分布
年龄/岁
13
14
15
16
频数
1
1
7
3
则该校女子排球队队员的平均年龄是 岁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角∠A是120°,第二次拐的角∠B是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C的大小是( )
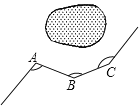
A.150° B.130° C.140° D.120°
相关试题

