【题目】在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=![]() ∠ABC.
∠ABC.

(1)如图1,以点B为旋转中心,将△EBC按顺时针方向旋转,得到△E′BA(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;
(2)如图2,若∠ABC=90°,AD=4,EC=2,求DE的长.
参考答案:
【答案】(1)见解析;(2)2![]() .
.
【解析】
试题分析:(1)先根据旋转的性质得BE′=BE,∠E′BA=∠EBC,则∠E′BE=∠ABC,再利用∠DBE=![]() ∠ABC易得∠DBE′=∠DBE,根据“SAS”判断△BDE′≌△BDE,所以DE′=DE;
∠ABC易得∠DBE′=∠DBE,根据“SAS”判断△BDE′≌△BDE,所以DE′=DE;
(2)以点B为旋转中心,将△EBC按顺时针方向旋转90°得到△E′BA(点C与点A重合,点E到点E′处),如图2,利用等腰直角三角形的性质得∠BCE=∠BAD=45°,利用旋转的性质得∠BAE′=∠BCE=45°,AE′=CE=2,则∠DAE′=90°,在Rt△DAE′中利用勾股定理可计算出DE′=2![]() ,然后就根据(1)的结论即可得到DE=DE′=2
,然后就根据(1)的结论即可得到DE=DE′=2![]() .
.
(1)证明:∵以点B为旋转中心,将△EBC按顺时针方向旋转,得到△E′BA(点C与点A重合,点E到点E′处),
∴BE′=BE,∠E′BA=∠EBC,
∴∠E′BE=∠ABC,
∵∠DBE=![]() ∠ABC,
∠ABC,
∴∠DBE=![]() ∠E′BE,即∠DBE′=∠DBE,
∠E′BE,即∠DBE′=∠DBE,
在△BDE′和△BDE中,
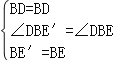 ,
,
∴△BDE′≌△BDE(SAS),
∴DE′=DE;
(2)解:以点B为旋转中心,将△EBC按顺时针方向旋转90°得到△E′BA(点C与点A重合,点E到点E′处),如图2,
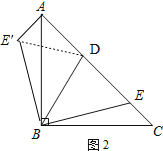
∵∠ABC=90°,BA=BC,
∴∠BCE=∠BAD=45°,
∵△EBC按顺时针方向旋转90°得到△E′BA,
∴∠BAE′=∠BCE=45°,AE′=CE=2,
∴∠DAE′=∠BAD+∠BAE′=90°,
在Rt△DAE′中,∵DE′2=AD2+AE′2=42+22=20,
∴DE′=2![]() ,
,
由(1)的结论得DE=DE′=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三张外观相同的卡片分别标有数字1、2、3,从中随机一次抽出两张,这两张卡片上的数字恰好都小于3的概率是( )
A. B. C. D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】张朋将连续10天引体向上的测试成绩(单位:个)记录如下:16,18,18,16,19,19,18,21,18,21.则这组数据的中位数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点B和点C分别为∠MAN两边上的点,AB=AC.
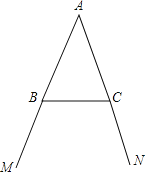
(1)按下列语句画出图形:
①AD⊥BC,垂足为D;
②∠BCN的平分线CE与AD的延长线交于点E;
③连接BE.
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形: ≌ , ≌ ;并选择其中的一对全等三角形,予以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要从甲、乙两名运动员中选出一名参加“2016里约奥运会”100m比赛,对这两名运动员进行了10次测试,经过数据分析,甲、乙两名运动员的平均成绩均为10.05(s),甲的方差为0.024(s2),乙的方差为0.008(s2),则这10次测试成绩比较稳定的是 运动员.(填“甲”或“乙”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校女子排球队队员的年龄分布
年龄/岁
13
14
15
16
频数
1
1
7
3
则该校女子排球队队员的平均年龄是 岁.
相关试题

