搜索
【题目】如图，在平面直角坐标系中，
的顶点均在正方形的格点上，点D的坐标是
，点A的坐标是
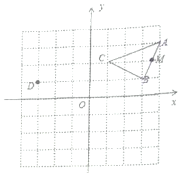
（1）将平移后使点C与点D重合，点A、B分别与点E、F重合，画出
，并直接写出E、F的坐标．
（2）若AB上的点M坐标为
，则平移后的对应点
的坐标为_______（用含x、y的代数式表示）
（3）求的面积.
参考答案：
【答案】（1）E（0,2），F（-1,0）（2）（x-4,y-1）（3）面积为2.5.
【解析】
（1）根据题意画出图形，根据直角坐标系即可写出坐标；
（2）根据平移的性质即可得到M’的坐标；
（3）根据割补法即可求出△ABC的面积.
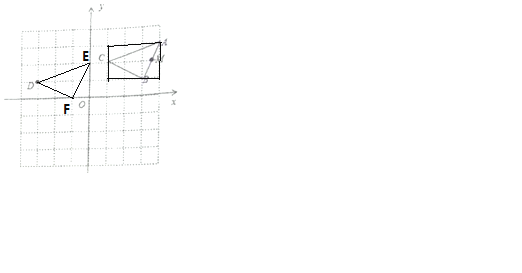
（1）如图，△DEF为所求，E（0,2），F（-1,0）
（2）平移后的对应点
的坐标为（x-4,y-1）
（3）△ABC的面积为
=2.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】（7分）如图，EF//AD，
＝
.求证：∠DGA+∠BAC=180°.请将说明过程填写完成.
证明：∵EF//AD，（已知）
∴
＝_____(_____________________________).又∵
＝
（______）∴
＝
（________________________）.∴AB//______(____________________________)
∴∠DGA+∠BAC=180°(_____________________________)
-
科目： 来源： 题型：
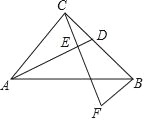
查看答案和解析>>【题目】已知：如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D是BC的中点，CE⊥AD，垂足为点E，BF∥AC交CE的延长线于点F．
求证：AC＝2BF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某年级380名师生秋游，计划租用7辆客车，现有甲、乙两种型号客车，它们的载客量和租金如表．
甲种客车
乙种客车
载客量（座/辆）
60
45
租金（元/辆）
550
450
（1）设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；
（2）当甲种客车有多少辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠B+∠ACB=30°，AB=4，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点，如图
（1）指出旋转中心，并求出旋转角的度数．
（2）求出∠BAE的度数和AE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB＝90°，点D、E分别在AB、AC上，且CE＝BC，连接CD，将线段CD绕点C按顺时针方向旋转90°后得到CF，连接EF．
（1）求证：△BDC≌△EFC；
（2）若EF∥CD，求证：∠BDC＝90°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，点C在∠AOB的一边OA上，过点C的直线DE∥OB，CF平分∠ACD，CG⊥CF于点C．
(1)若∠O＝40°，求∠ECF的度数；
(2)求证：CG平分∠OCD．
相关试题
