【题目】如图,矩形![]() 中,点
中,点![]() 分别在边
分别在边![]() 与
与![]() 上,点
上,点![]() 在对角线
在对角线![]() 上,
上,![]() ,
,![]() .
.
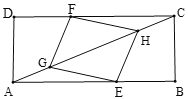
![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见详解;(2)5
【解析】
(1)依据矩形的性质,即可得出△AEG≌△CFH,进而得到GE=FH,∠CHF=∠AGE,由∠FHG=∠EGH,可得FH∥GE,即可得到四边形EGFH是平行四边形;
(2)由菱形的性质,即可得到EF垂直平分AC,进而得出AF=CF=AE,设AE=x,则FC=AF=x,DF=8-x,依据Rt△ADF中,AD2+DF2=AF2,即可得到方程,即可得到AE的长.
解:(1)∵矩形ABCD中,AB∥CD,
∴∠FCH=∠EAG,
又∵CD=AB,BE=DF,
∴CF=AE,
又∵CH=AG,
∴△AEG≌△CFH,
∴GE=FH,∠CHF=∠AGE,
∴∠FHG=∠EGH,
∴FH∥GE,
∴四边形EGFH是平行四边形;
(2)如图,连接EF,AF,
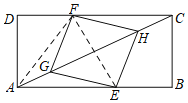
∵EG=EH,四边形EGFH是平行四边形,
∴四边形GFHE为菱形,
∴EF垂直平分GH,
又∵AG=CH,
∴EF垂直平分AC,
∴AF=CF=AE,
设AE=x,则FC=AF=x,DF=8-x,
在Rt△ADF中,AD2+DF2=AF2,
∴42+(8-x)2=x2,
解得x=5,
∴AE=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A(2,4),B(1,1),C(5,2).

(1)在如图所示的平面直角坐标系中描出各点,画出三角形ABC;
(2)将三角形ABC向左平移6个单位,再向下平移3个单位,请在图中作出平移后的三角形A1B1C1;
(3)写出三角形各点A1、B1、C1的坐标;
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线
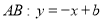 分别与
分别与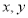 轴交于
轴交于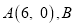 两点,过点
两点,过点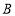 的直线交
的直线交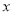 轴负半轴于
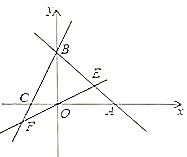
轴负半轴于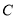 ,且
,且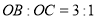 .
.
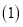 求点
求点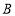 坐标.
坐标.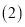 求直线
求直线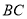 的解析式.
的解析式.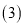 直线
直线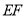 的解析式为
的解析式为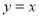 ,直线
,直线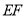 交
交 于点
于点 ,交
,交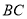 于点
于点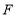 ,求证:
,求证: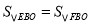 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(1,4),B(1,1),C(3,1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一道证明题,李老师已给同学们讲解了思路.请你将过程和理由补充完整.
已知∠1=∠2,∠A=∠E. 求证:AD∥BE.
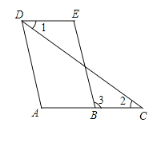
证明:∵∠1=∠2 (已知)
∴AC∥________(___________________________________)
∴∠3= _______ (___________________________________)
又∵∠A=∠E(___________)
∴∠A=______(___________________)
∴AD∥BE (_________________________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校体育组对本校九年级全体同学体育测试情况进行调查,他们随机抽查部分同学体育测试成绩(由高到低分
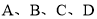 四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.
四个等级),根据调查的数据绘制成如下的条形统计图和扇形统计图.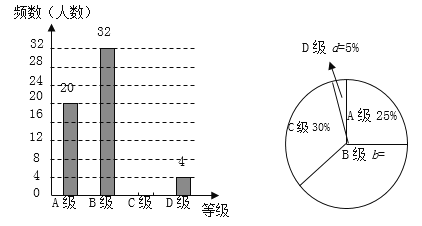
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)该校体育组共抽查了多少名同学的体育测试成绩?扇形统计图中B级所占的百分比b等于多少?
(2)补全条形统计图;
(3)若该校九年级共有200名同学,请估计该校九年级同学体育测试达标(测试成绩C级以上,含C级)约有多少名?
相关试题

