【题目】在△ABC 中,AB = 13,AC = 20,BC 边上的高为12,则BC 的长为_______.
参考答案:
【答案】21或11
【解析】分两种情况:①∠B为锐角;②∠B为钝角;利用勾股定理求出BD、CD,即可求出BC的长.
解:分两种情况:①当∠B为锐角时,如图1所示,

在Rt△ABD中,
BD=![]() =5(cm),
=5(cm),
在Rt△ADC中,
CD=![]() =16cm,
=16cm,
∴BC=BD+CD=21cm;
②当∠B为钝角时,如图2所示,

在Rt△ABD中,
BD=![]() =5(cm),
=5(cm),
在Rt△ADC中,
CD=![]() =16cm,
=16cm,
∴BC=CD﹣BD=16﹣5=11(cm);
综上所述:BC的长为21cm或11cm.
“点睛”本题考查了勾股定理,把三角形斜边转化到直角三角形中用勾股定理解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把a3﹣ab2分解因式的结果为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为提倡节约用水,采取分段收费,若用户每月用水不超过20立方米,每立方米收费2元;若用水超过20立方米,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水量为( )
A. 34立方米 B. 32立方米 C. 30立方米 D. 28立方米
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=mx2+x﹣2m(m是非0常数)的图象与x轴的交点个数为( )
A.0个
B.1个
C.2个
D.1个或2个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线
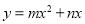 相交于A(1,
相交于A(1,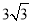 ),B(4,0)两点.
),B(4,0)两点.(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出
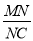 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.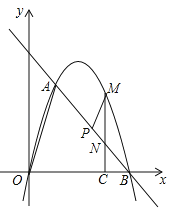
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:2(a+1)﹣a=
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.
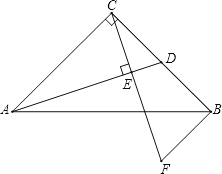
(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
相关试题

