【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是 . 
参考答案:
【答案】6﹣π
【解析】解:

过F作FM⊥BE于M,则∠FME=∠FMB=90°,
∵四边形ABCD是正方形,AB=2,
∴∠DCB=90°,DC=BC=AB=2,∠DCB=45°,
由勾股定理得:BD=2 ![]() ,
,
∵将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,
∴∠DCE=90°,BF=BD=2 ![]() ,∠FBE=90°﹣45°=45°,
,∠FBE=90°﹣45°=45°,
∴BM=FM=2,ME=2,
∴阴影部分的面积S=S△BCD+S△BFE+S扇形DCE﹣S扇形DBF
= ![]() +
+ ![]() +
+ ![]() ﹣
﹣ ![]()
=6﹣π,
所以答案是:6﹣π.
【考点精析】通过灵活运用正方形的性质和扇形面积计算公式,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,点A(0,0)、B(4
 ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1 , 第2个△B1A2B2 , 第3个△B2A3B3 , …则第2017个等边三角形的边长等于( ) 
A.
B.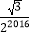
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是
 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A. 2,
 B. 2,1 C. 4,
B. 2,1 C. 4, D. 4,3
D. 4,3 -
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐___________人;当有
 张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).(2)一天中午,餐厅要接待85位顾客共同就餐,但餐厅中只有20张这样的长方形桌子可用,且每4张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:

(说明:成绩80分及以上为生产技能优秀,70-79分为生产技能良好,60-69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
得出结论:
a.估计乙部门生产技能优秀的员工人数为________;
b.可以推断出________部门员工的生产技能水平较高,理由为________.(至少从两个不同的角度说明推断的合理性)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=10,AC=16,点M是对角线AC上的一个动点,过点M作PQ⊥AC交AB于点P,交AD于点Q,将△APQ沿PQ折叠,点A落在点E处,当△BCE是等腰三角形时,AP的长为

相关试题

