搜索
【题目】如图，在ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=3，EF=1，则BC长为（ ）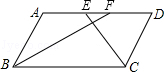 
A.4
B.5
C.6
D.7
参考答案：
【答案】B
【解析】解：∵四边形ABCD是平行四边形， ∴AB=CD=3，BC=AD，AD∥BC，
∵BF平分∠ABC交AD于E，CE平分∠BCD交AD于F，
∴∠ABF=∠CBF=∠AFB，∠BCE=∠DCE=∠CED，
∴AB=AF=3，DC=DE=3，
∴EF=AF+DE﹣AD=3+3﹣AD=1．
∴AD=5，
∴BC=5
故选：B．
【考点精析】关于本题考查的平行四边形的性质，需要了解平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，点D、E在BC上，连接AD、AE，如果只添加一个条件使∠DAB=∠EAC，则添加的条件不能为（ ）
A. BD=CE B. AD=AE C. DA=DE D. BE=CD
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2﹣10x+16=0的两个根，且抛物线的对称轴是直线x=﹣2．
（1）求A、B、C三点的坐标；
（2）求此抛物线的表达式；
（3）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；
（4）在（3）的基础上试说明S是否存在最大值？若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，点D是BC的中点，点E在AD上．
求证：（1）△ABD≌△ACD；
（2）BE=CE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】读题画图计算并作答
画线段AB＝3 cm，在线段AB上取一点K，使AK＝BK，在线段AB的延长线上取一点C，使AC＝3BC，在线段BA的延长线取一点D，使AD＝
AB.(1)求线段BC、DC的长？
(2)点K是哪些线段的中点？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△P1OA1 ， △P2A1A2都是等腰直角三角形，点P1 ， P2都在函数y=
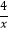（x＞0）的图象上，斜边OA1、A1A2都在x轴上，则点P2的坐标是（ ）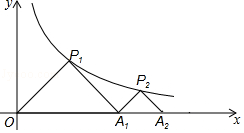 
A.（4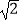
， ）
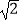B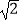.（4+2 ，4﹣2 ）??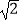
C.（2+2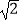 ，2 ﹣2）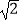
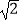D.（4+2 ，2+2 ） -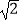
科目： 来源： 题型：
查看答案和解析>>【题目】七年级⑴班想买一些运动器材供班上同学阳光体育活动使用，班主任安排班长去商店买篮球和排球，下面是班长与售货员的对话：
班长：阿姨，您好！ 售货员：同学，你好，想买点什么？
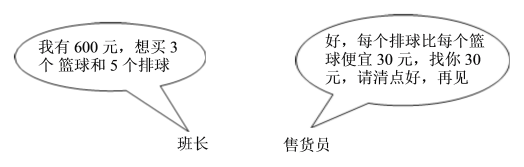
⑴根据这段对话，你能算出篮球和排球的单价各是多少吗？
⑵六一儿童节店里搞活动有两种套餐，1、套装打折：五个篮球和五个排球为一套装，套装打 八折：2、满减活动：999 减 100，1999 减 200；两种活动不重复参与，学校需要 15个篮球，13 个排球作为奖品，请问如何安排购买更划算？
相关试题
