【题目】已知方程组![]() 的解x为非正数,y为负数.
的解x为非正数,y为负数.
(1)求a的取值范围;
(2)化简∣a-3∣+∣a+2∣;
(3).教科书中这样写道:“我们把多项式a2+2ab+b2及a2-2ab+b2叫做完全平方式.”如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值、最小值等.
例如:分解因式x2+2x-3=(x2+2x+1)-4=(x+1)2-4=(x+1)2-4=(x+1+2)(x+1-2)=(x+3)(x-1);
根据阅读材料用配方法解决下列问题:
①分解因式:m2-4m-5=
②当a,b为何值时,多项式a2+b2-4a+6b+13=0.
③当a,b为何值时,多项式a2-2ab+2b2-2a-4b+10=0.
参考答案:
【答案】(1) ![]() ;(2)5;(3)①(m-5)(m+1);②当a=2,b=﹣3时;③当a=4,b=3时,原式=0
;(2)5;(3)①(m-5)(m+1);②当a=2,b=﹣3时;③当a=4,b=3时,原式=0
【解析】
(1)直接求解,得到含有a的解,然后根据题干给出的x为非正数,y为负数,得到关于a的一元一次不等式组,求出解集即可.
(2)由(1)知a的范围,再判断出a-3,a+2的正负,再去括号.
(3)①根据题干中配方法的特点把m2﹣4m﹣5=m2﹣4m+4﹣9,再去运用完全平方差公式.
②把原式中的13化为![]() ,再结合成两个完全平方式,利于非负数的性质求解.
,再结合成两个完全平方式,利于非负数的性质求解.
③把原始中-2ab -2a结合得到-2a(b+1),然后与a2配方![]() ,最后化简整理与剩下的单项式得到另一个完全平方式,最后求解.
,最后化简整理与剩下的单项式得到另一个完全平方式,最后求解.
(1)解方程组![]() 得
得![]() 由题意,得
由题意,得![]() 解得
解得![]() .
.
(2)∵![]() ,∴
,∴![]() ,
,![]()
则![]() =3-a+(a+2)=5
=3-a+(a+2)=5
(3)
①m2﹣4m﹣5=m2﹣4m+4﹣9=(m﹣2)2﹣9 =(m﹣2+3)(m﹣2﹣3)
=(m+1)(m﹣5).
②∵a2+b2﹣4a+6b+13=(a﹣2)2+(b+3)2,
∴当a=2,b=﹣3时,原式为0.
③∵a2﹣2ab+2b2﹣2a﹣4b+10=0
则![]()

即![]()
则![]() 时,原式为0.
时,原式为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
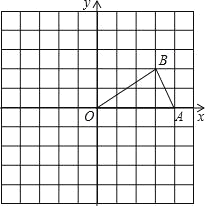
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是________.(写出正确命题的序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数 y kx b 的图象与 x 轴交点为 A3, 0,与 y 轴交点为 B ,且与正比例函数
 的图象交于点C(m,4).
的图象交于点C(m,4).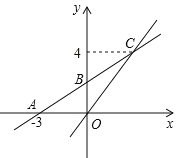
(1)求点C 的坐标;
(2)求一次函数 y kx b 的表达式;
(3)若点 P 是 y 轴上一点,且BPC 的面积为 6,请直接写出点 P 的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线
 的一部分,如图
的一部分,如图
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并解决问题:
 如图
如图 等边
等边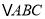 内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求
内有一点P,若点P到顶点A、B、C的距离分别为3,4,5,求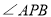 的度数.为了解决本题,我们可以将
的度数.为了解决本题,我们可以将 绕顶点A旋转到
绕顶点A旋转到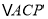 处,此时
处,此时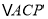 ≌
≌ ,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出
,这样就可以利用旋转变换,将三条线段PA、PB、PC转化到一个三角形中,从而求出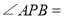 ______;
______; 基本运用
基本运用
请你利用第
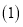 题的解答思想方法,解答下面问题:已知如图
题的解答思想方法,解答下面问题:已知如图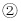 ,
,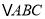 中,
中,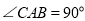 ,
,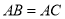 ,E、F为BC上的点且
,E、F为BC上的点且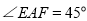 ,求证:
,求证: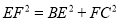 ;
;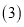 能力提升
能力提升如图
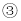 ,在
,在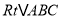 中,
中,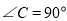 ,
,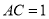 ,
,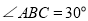 ,点O为
,点O为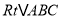 内一点,连接AO,BO,CO,且
内一点,连接AO,BO,CO,且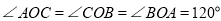 ,求
,求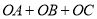 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
相关试题

