【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论是________.(写出正确命题的序号)

参考答案:
【答案】①④
【解析】试题解析:由二次函数图象开口向上,得到a>0;与y轴交于负半轴,得到c<0,
∵对称轴在y轴右侧,且![]() 即2a+b=0,
即2a+b=0,
∴a与b异号,即b<0,
∴abc>0,选项①正确;
∵二次函数图象与x轴有两个交点,
![]() 即
即![]() ,选项②错误;
,选项②错误;
∵原点O与对称轴的对应点为(2,0),
∴x=2时,y<0,即4a+2b+c<0,选项③错误;
∵x=1时,y>0,
∴ab+c>0,
把b=2a代入得:3a+c>0,选项④正确,
故答案为:①④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( )

A. 1 m B. 2 m C. 3 m D. 6 m
-
科目: 来源: 题型:
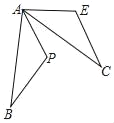
查看答案和解析>>【题目】(1)如图,△AEC绕A点顺时针旋转60°得△APB,∠PAC=20°,求∠BAE.
(2)解不等式组:
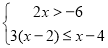
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
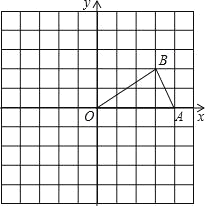
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数 y kx b 的图象与 x 轴交点为 A3, 0,与 y 轴交点为 B ,且与正比例函数
 的图象交于点C(m,4).
的图象交于点C(m,4).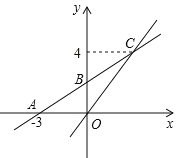
(1)求点C 的坐标;
(2)求一次函数 y kx b 的表达式;
(3)若点 P 是 y 轴上一点,且BPC 的面积为 6,请直接写出点 P 的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
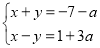 的解x为非正数,y为负数.
的解x为非正数,y为负数.(1)求a的取值范围;
(2)化简∣a-3∣+∣a+2∣;
(3).教科书中这样写道:“我们把多项式a2+2ab+b2及a2-2ab+b2叫做完全平方式.”如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值、最小值等.
例如:分解因式x2+2x-3=(x2+2x+1)-4=(x+1)2-4=(x+1)2-4=(x+1+2)(x+1-2)=(x+3)(x-1);
根据阅读材料用配方法解决下列问题:
①分解因式:m2-4m-5=
②当a,b为何值时,多项式a2+b2-4a+6b+13=0.
③当a,b为何值时,多项式a2-2ab+2b2-2a-4b+10=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线
 的一部分,如图
的一部分,如图
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
相关试题

