搜索
【题目】如图，把△ABC向上平移4个的那位长度，再向右平移3个单位长度，得到△A′B′C′．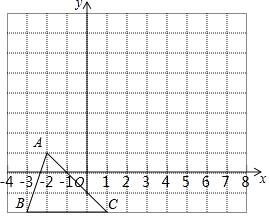
（1）在图中画出△A′B′C′；
（2）连接A′A、C′C，求四边形A′AC′C的面积．
参考答案：
【答案】
（1）解：如图所示：△A′B′C′即为所求；
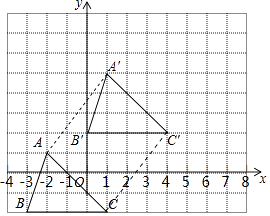
（2）解：S四边形A'AC'C=S△A′CC′+S△A′CA= 
×7×3+ ×7×3=21．
【解析】（1）根据图形平移的性质画出平移后的△A′B′C′即可；
（2）利用S四边形A'AC'C=S△A′CC′+S△A′CA即可得出结论．
【考点精析】根据题目的已知条件，利用坐标与图形变化-平移的相关知识可以得到问题的答案，需要掌握新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点；连接各组对应点的线段平行且相等．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知反比例函数y=﹣
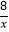， 则有
①它的图象在一、三象限：
②点（﹣2，4）在它的图象上；
③当l＜x＜2时，y的取值范围是﹣8＜y＜﹣4；
④若该函数的图象上有两个点A （x1 ， y1），B（x2 ， y2），那么当x1＜x2时，y1＜y2
以上叙述正确的是 -
科目： 来源： 题型：
查看答案和解析>>【题目】﹣27的立方根与4的平方根的和是_____
-
科目： 来源： 题型：
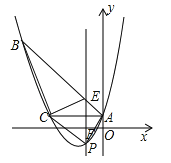
查看答案和解析>>【题目】如图，已知抛物线
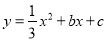经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．（1）求抛物线的解析式；
（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；
（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．
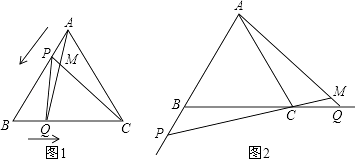
（1）求证：△ABQ≌△CAP；
（2）如图1，当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说理由；若不变，求出它的度数．
（3）如图2，若点P、Q在分别运动到点B和点C后，继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC=度．（直接填写度数） -
科目： 来源： 题型：
查看答案和解析>>【题目】先化简，后求值：
，其中x在数轴上的对应点到原点的距离为 
个单位长度． -
科目： 来源： 题型：
查看答案和解析>>【题目】方程x2=2x的根是（ ）
A.x=2
B.x=﹣2
C.x1=0，x2=2
D.x1=0，x2=﹣2
相关试题
