【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°. 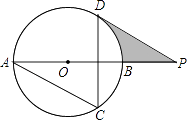
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OD,
∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°,
∴∠DOP=180°﹣120°=60°,
∵∠APD=30°,
∴∠ODP=180°﹣30°﹣60°=90°,
∴OD⊥DP,
∵OD为半径,
∴DP是⊙O切线
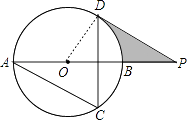
(2)解:∵∠P=30°,∠ODP=90°,OD=3cm,
∴OP=6cm,由勾股定理得:DP=3 ![]() cm,
cm,
∴图中阴影部分的面积S=S△ODP﹣S扇形DOB= ![]() ×3×3
×3×3 ![]() ﹣
﹣ ![]() =(
=( ![]()
![]() ﹣
﹣ ![]() π)cm2
π)cm2
【解析】(1)连接OD,求出∠AOD,求出∠DOB,求出∠ODP,根据切线判定推出即可;(2)求出OP、DP长,分别求出扇形DOB和三角形ODP面积,即可求出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:( )﹣1+|3tan30°﹣1|﹣(π﹣3)0;
)﹣1+|3tan30°﹣1|﹣(π﹣3)0;
(2)先化简,再求值:
 ,其中x=
,其中x=  ﹣3.
﹣3. -
科目: 来源: 题型:
查看答案和解析>>【题目】保障房建设是民心工程,某市从2008年开始加快保障房建设进程,现统计了该市2008年到2012年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.

(1)小丽看了统计图后说:“该市2011年新建保障房的套数比2010年少了.”你认为小丽说法正确吗?请说明理由;
(2)求补全条形统计图;
(3)求这5年平均每年新建保障房的套数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
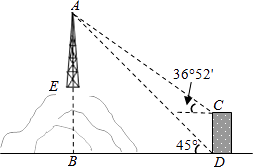
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).

(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.

(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;
(3)若AD=10,AB=a,DP=8,随着a的大小的变化,点M的位置也在变化.当点M落在矩形ABCD外部时,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的二次函数y=﹣x2+ax(a>0),点A(n,y1)、B(n+1,y2)、C(n+2,y3)都在这个二次函数的图象上,其中n为正整数.
(1)y1=y2 , 请说明a必为奇数;
(2)设a=11,求使y1≤y2≤y3成立的所有n的值;
(3)对于给定的正实数a,是否存在n,使△ABC是以AC为底边的等腰三角形?如果存在,求n的值(用含a的代数式表示);如果不存在,请说明理由.
相关试题

