【题目】在平面直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:
如果y′= ![]() ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
例如:点(5,6)的“关联点”为点(5,6),点(﹣5,6)的“关联点”
为点(﹣5,﹣6).
(1)①点(2,1)的“关联点”为;②如果点A(3,﹣1),B(﹣1,3)的“关联点”中有一个在函数 ![]() 的图象上,那么这个点是(填“点A”或“点B”).
的图象上,那么这个点是(填“点A”或“点B”).
(2)①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”,
那么点M的坐标为;②如果点N*(m+1,2)是一次函数y=x+3图象上点N的“关联点”,求点N的坐标 .
(3)如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,其“关联点”Q的纵坐标
y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是 . 
参考答案:
【答案】
(1)(2,1),B
(2)(﹣1,2),(﹣1,﹣2)
(3)-2<a<2.
【解析】解:(1)①点(2,1)的“关联点”为(2,1);
②如果点A(3,﹣1)的关联点为(3,﹣1);
B(﹣1,3)的“关联点”为(﹣1,﹣3),
一个在函数y=![]() 图象上,那么这个点是 B;
图象上,那么这个点是 B;
所以答案是:(2,1),B;
( 2 )①如果点M*(﹣1,﹣2)是一次函数y=x+3图象上点M的“关联点”是(﹣1,2),
那么点M的坐标为(﹣1,2);②如果点N*(m+1,2)是一次函数y=x+3图象上,
点N*(﹣1,2)的“关联点”(﹣1,﹣2),
点N的坐标是(﹣1,﹣2),
所以答案是:(﹣1,2),(﹣1,﹣2);
( 3 )如果点P在函数y=﹣x2+4(﹣2<x≤a)的图象上,
当﹣2<x≤0时,0<y≤4,即﹣2<a≤0;
当x>0时,y=y′,即﹣4<y≤4,
﹣x2+4>﹣4,解得x<2 ![]() ,
,
即0<x<2 ![]() ,
,
综上所述:﹣2<x<2 ![]() ,
,
﹣2<a<2 ![]() .
.
“关联点”Q的纵坐标y′的取值范围是﹣4<y′≤4,那么实数a的取值范围是﹣2<a<2 ![]() ,
,
所以答案是:﹣2<a<2.
【考点精析】关于本题考查的一次函数的性质和二次函数的图象,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
 经过点A(0,2)和B(1,
经过点A(0,2)和B(1,  ).
).
(1)求该抛物线的表达式;
(2)已知点C与点A关于此抛物线的对称轴对称,点D在抛物线上,且点D的横坐标为4,求点C与点D的坐标;
(3)在(2)的条件下,将抛物线在点A,D之间的部分(含点A,D)记为图象G,如果图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平整的地面上,10个完全相同的棱长为8cm的小正方体堆成一个几何体.
(1)在下面的网格中画出从左面看和从上面看的形状图.
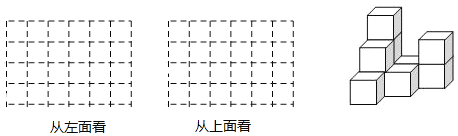
(2)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)已知A=3x2+4xy,B=x2+3xy--y2,求:-A+2B.
(2)先化简,再求值:2(5a2-7ab+9b2)-3(14a2-2ab+3b2),其中a=
 ,b=-
,b=- .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.

被调查的捐款人数分组统计表:
组别
捐款额x/元
人数
A
1≤x<10
a
B
10≤x<20
100
C
20≤x<30
______
D
30≤x<40
______
E
40≤x
______
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠BAD=120°,射线AP位于该菱形外侧,点B关于直线AP的对称点为E,连接BE、DE,直线DE与直线AP交于F,连接BF,设∠PAB=α.
(1)依题意补全图1;
(2)如图1,如果0°<α<30°,判断∠ABF与∠ADF的数量关系,并证明;
(3)如图2,如果30°<α<60°,写出判断线段DE,BF,DF之间数量关系的思路;(可以不写出证明过程)
(4)如果60°<α<90°,直接写出线段DE,BF,DF之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】小刚在实践课上要做一个如图1所示的折扇,折扇扇面的宽度AB是骨柄长OA的
 ,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24
,折扇张开的角度为120°.小刚现要在如图2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料长为24  cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )
cm,宽为21cm.小刚经过画图、计算,在矩形布料上裁剪下了最大的扇面,若不计裁剪和粘贴时的损耗,此时扇面的宽度AB为( )
A.21cm
B.20 cm
C.19cm
D.18cm
相关试题

