【题目】如图1,直线AB上有一点P,点M、N分别为线段PA、PB的中点,AB=14.
(1)若点P在线段AB上,且AP=8,求线段MN的长度;
(2)若点P在直线AB上运动,设AP=x,BP=y,请分别计算下面情况时MN的长度:
①当P在AB之间(含A或B);
②当P在A左边;
③当P在B右边;
你发现了什么规律?
(3)如图2,若点C为线段AB的中点,点P在线段AB的延长线上,下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,请选择一个正确的结论并求其值.
的值不变,请选择一个正确的结论并求其值.
图1
![]() ,
,
图2
![]() ,
,
参考答案:
【答案】(1)7.(2)①点P在AB之间,MN=![]() (x+y);②点P在A左边,MN=
(x+y);②点P在A左边,MN=![]() (y-x);③点P在BA的延长线上,MN=
(y-x);③点P在BA的延长线上,MN=![]() (x-y);(3)选择②①
(x-y);(3)选择②①![]() =
=![]() (在变化);②
(在变化);②![]() =2
=2
【解析】
(1)由AP=8且点M是AP的中点易得MP=![]() AP=4,BP=AB-AP=6,再由点N是PB的中点可知PN=
AP=4,BP=AB-AP=6,再由点N是PB的中点可知PN=![]() PB=3,则MN=MP+PN=7;
PB=3,则MN=MP+PN=7;
(2)根据线段中点的性质,可得MP和NP的表达式,再根据线段的和差关系分别计算三种情况下MN的长度即可;
(3)根据线段的和差,分别可得PA-PB=AB,PA+PB=PC+AC+PC-BC=2PC,再根据分式的性质即可判断.
解:(1)∵AP=8,点M是AP的中点,
∴MP=![]() AP=4,
AP=4,
∴BP=AB-AP=6.
又∵点N是PB的中点,
∴PN=![]() PB=3,
PB=3,
∴MN=MP+PN=7.
(2)①点P在AB之间,MN=MP+PN=![]() =
=![]() (x+y);
(x+y);
②点P在A左边,MN=PN-MP=![]() -
-![]() =
=![]() (y-x);
(y-x);
③点P在BA的延长线上,MN=MP-PN=![]() -
-![]() ==
==![]() (x-y).
(x-y).
(3)选择②.
①![]() ,由于PC长度不固定,故
,由于PC长度不固定,故![]() 的值是变化的;
的值是变化的;
②![]() ,是定值,
,是定值,
故正确的结论是②,其值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5


5≤x<6
10
20%
6≤x<7

12%
7≤x<8
3
6%
8≤x<9
2
4%

(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,CE⊥AB于点E,BD⊥AC于点D,BD,CE交于点O,且AO平分∠BAC,则图中的全等三角形共有________对.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,
 ∠BOD=∠DOE.
∠BOD=∠DOE.(1)求∠BOF的度数;
(2)请写出图中与∠BOD相等的所有的角.

-
科目: 来源: 题型:
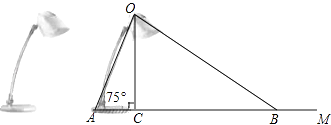
查看答案和解析>>【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,
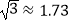 ).
). 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k<0)与反比例函数y=
 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1) 
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的个数是( )
(1)﹣a表示负数;
(2)多项式﹣3a2b+7a2b2﹣2ab+l的次数是3;
(3)单项式﹣
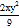 的系数为﹣2;
的系数为﹣2;(4)一个有理数不是整数就是分数
A. 0个 B. 1个 C. 2个 D. 3个
相关试题

