【题目】如图,是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面宽8cm,水的最大深度为2cm,求该输水管的半径是多少? 
参考答案:
【答案】解:过点O做OC⊥AB于点D,连接OA.
设半径长为rcm,
∵OC⊥AB,
∴AD= ![]() AB
AB
= ![]() ×8
×8
=4(cm),
∵CD=2cm∴OD=r﹣2(cm)
在Rt△AOD中,由勾股定理得:(r﹣2)2+42=r2
r2﹣4r+4+42=42
4r=20
r=5,
答:该水管的半径是5cm.
【解析】先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD= ![]() AB,设OA=r,则OD=r﹣2,在Rt△AOD中,利用勾股定理即可求出r的值.
AB,设OA=r,则OD=r﹣2,在Rt△AOD中,利用勾股定理即可求出r的值.
【考点精析】通过灵活运用垂径定理的推论,掌握推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
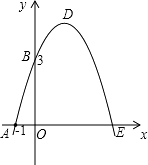
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级(1)班第1小组的每位同学都向“希望工程”捐献图书,捐书情况如下表:

(1)这个小组的每位同学平均捐献了多少册图书?
(2)求捐献图书册数的中位数和众数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE.

(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD的外接圆的直径. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)x2+6x﹣1=0
(2)(2x+3)2﹣25=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,∠AOF=∠BOF=90°.则
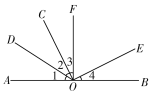
(1)∠AOC的补角是_____;
(2)____是∠AOC的余角;
(3)∠COF的补角是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1 , y1),B(x2 , y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
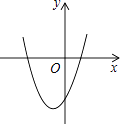
A.y1<y2
B.y1>y2
C.y的最小值是﹣3
D.y的最小值是﹣4
相关试题

