【题目】如图,在Rt△ABC中,∠ACB=90,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE. 
(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD的外接圆的直径.
参考答案:
【答案】
(1)证明:∵AD平分∠BAC,
∴∠CAD=∠EAD,
∴ ![]() =
= ![]() ,
,
∴CD=ED
∵∠ACD=90°,
∴AD是⊙O的直径,
∴ ![]() =
= ![]() ,
,
∴AC=AE
(2)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB= ![]() =10,
=10,
BE=10﹣AE=10﹣6=4,
设CD=DE=x,
BD=8﹣x,
在Rt△BDE中.BD2=DE2+BE2
(8﹣x)2+x2=42
x=3,即BD=3,
在Rt△ACD中,AD= ![]() =3
=3 ![]()
【解析】(1)根据角平分线的性质、圆周角、弧、弦之间的关系得到 ![]() =
= ![]() ,证明结论;(2)根据勾股定理求出AB,设CD=DE=x,根据勾股定理列出方程,求出x,计算即可.
,证明结论;(2)根据勾股定理求出AB,设CD=DE=x,根据勾股定理列出方程,求出x,计算即可.
【考点精析】认真审题,首先需要了解三角形的外接圆与外心(过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某俱乐部篮球队队员年龄结构直方图,根据图中信息解答下列
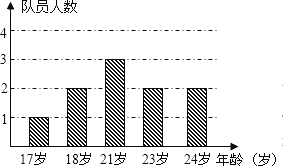
问题:
(1)该队队员年龄的平均数;
(2)该队队员年龄的众数和中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
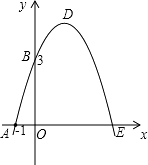
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级(1)班第1小组的每位同学都向“希望工程”捐献图书,捐书情况如下表:

(1)这个小组的每位同学平均捐献了多少册图书?
(2)求捐献图书册数的中位数和众数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面宽8cm,水的最大深度为2cm,求该输水管的半径是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)x2+6x﹣1=0
(2)(2x+3)2﹣25=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,∠AOF=∠BOF=90°.则
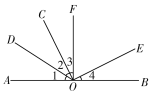
(1)∠AOC的补角是_____;
(2)____是∠AOC的余角;
(3)∠COF的补角是___.
相关试题

