【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)当BC=AF时,四边形ABFC是矩形.理由见解析.
【解析】试题分析:
(1)利用平行四边形的性质得出∠BAF=∠CFA,进而得出△AEB≌△FEC(AAS),求出答案;
(2)首先得出四边形ABFC是平行四边形,进而得出答案.
试题解析:
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF.
∴∠BAF=∠CFA.
∵E为BC的中点,
∴BE=CE.
又∵∠AEB=∠FEC,
∴△AEB≌△FEC(AAS).
∴AB=CF.
(2)当BC=AF时,四边形ABFC是矩形.理由如下:
由(1),得AB=CF,
∵AB∥CF,
∴四边形ABFC是平行四边形.
∵BC=AF,
∴四边形ABFC是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+3经过点(2,-3),则该直线的函数关系式是____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果抛物线y=(a+2)x2+x﹣1的开口向下,那么a的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式5﹣2x>﹣3的解集是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
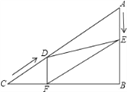
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)判断四边形EFGH的形状,并证明你的结论;
(2)当BD,AC满足什么条件时,四边形EFGH是正方形.(不要求证明)

-
科目: 来源: 题型:
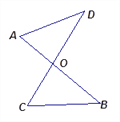
查看答案和解析>>【题目】如图:线段AB、CD相交于点O,连接AD、CB,我们把这个图形称为“8字型”.
根据三角形内角和容易得到:∠A+∠D=∠C+∠B.
⑴利用“8字型”
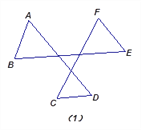
如图(1):∠A+∠B+∠C+∠D+∠E+∠F=_________.
⑵构造“8字型”
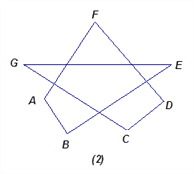
如图(2):∠A+∠B+∠C+∠D+∠E+∠F+∠G=_________.
⑶发现“8字型”
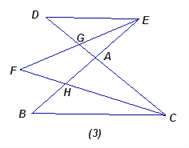
如图(3):BE、CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
①图中共有________个“8字型”;
②若∠B:∠D:∠F=4:6:x,求x的值.
相关试题

