【题目】如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( ) 
A.20°
B.30°
C.40°
D.50°
参考答案:
【答案】C
【解析】解:如下图所示,连接BC, 
∵AB 是直径,
∴∠BCA=90°,
又∵∠A=25°,
∴∠CBA=90°﹣25°=65°,
∵DC是切线,
∴∠BCD=∠A=25°,
∴∠D=∠CBA﹣∠BCD=65°﹣25°=40°.
故选C.
【考点精析】掌握圆周角定理和切线的性质定理是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B.C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①探究BD与CF之间的位置关系,并说明理由;
②当AB= ,AD=
,AD=  +1时,求线段DH的长.
+1时,求线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A.B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.

(1)求A,B,C,D的坐标;
(2)判断以点A,C,D为顶点的三角形的形状,并说明理由;
(3)点M( m,0)(﹣3<m<﹣1)为线段AB上一点,过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,得矩形PQNM,当矩形PQMN的周长最大时,m的值是多少?并直接写出此时△AEM的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )

A.10π
B.15π
C.20π
D.30π -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
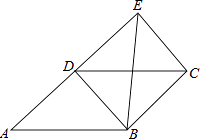
A.AB=BE
B.BE⊥DC
C.∠ADB=90°
D.CE⊥DE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:二次函数y=ax2+bx+c的图像所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):﹣6,﹣3,x,2,﹣1,3,若这组数据的中位数是﹣1,在下列结论中:①方差是8;②极差是9;③众数是﹣1;④平均数是﹣1,其中正确的序号是 .
相关试题

