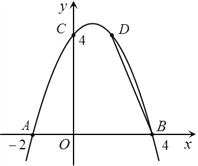
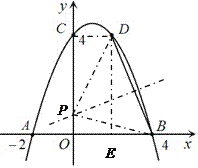
【题目】如图, 已知抛物线![]() 经过A(-2,0)、B(4,0)、C(0,4)三点.
经过A(-2,0)、B(4,0)、C(0,4)三点.
(1)求此抛物线的解析式;
(2)此抛物线有最大值还是最小值?请求出其最大或最小值;
(3)若点D(2,m)在此抛物线上,在y轴的正半轴上是否存在点P,使得△BDP是等腰三角形?若存在,请求出所有符合条件的P点的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() ;(3)符合条件的
;(3)符合条件的![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
【解析】分析:(1)将A(-2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c,运用待定系数法即可求出此抛物线的解析式;
(2)由于二次项系数a=-![]() <0,所以抛物线有最大值,最大值为
<0,所以抛物线有最大值,最大值为![]() ,代入计算即可;
,代入计算即可;
(3)先将点D(2,m)代入(1)中所求的抛物线的解析式,求出m的值,得到点D的坐标,然后假设在y轴的正半轴上存在点P(0,y)(y>0),使得△BDP是等腰三角形,再分三种情况进行讨论:①PB=PD;②BP=BD;③DP=DB;每一种情况都可以根据两点间的距离公式列出关于y的方程,解方程即可.
详解:(1)将A(-2,0)、B(4,0)、C(0,4)代入y=ax2+bx+c,得
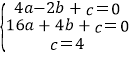 ,
,
解得: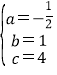 ,
,
所以此抛物线的解析式为y=-![]() x2+x+4;
x2+x+4;
(2)∵y=-![]() x2+x+4,a=-
x2+x+4,a=-![]() <0,
<0,
∴抛物线有最大值,最大值为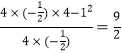 ;
;
(3)∵点D(2,m)在抛物线y=-![]() x2+x+4上,
x2+x+4上,
∴m=-![]() ×22+2+4=4,
×22+2+4=4,
∴D(2,4),
∵B(4,0),
∴BD=![]() .
.
假设在y轴的正半轴上存在点P(0,y)(y>0),使得△BDP是等腰三角形,分三种情况:
①如果PB=PD,那么42+y2=22+(y-4)2,解得y=![]() ,
,
所以P1(0,![]() );
);
②如果BP=BD,那么42+y2=20,解得y=±2(负值舍去),
所以P2(0,2);
③如果DP=DB,那么22+(y-4)2=20,解得y=0或8,
y=0不合题意舍去,
y=8时,(0,8)与D,B三点共线,不合题意舍去;
综上可知,所有符合条件的P点的坐标为P1(0,![]() ),P2(0,2).
),P2(0,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】公园内要铺设一段长方形步道,须用一些型号相同的灰色正方形地砖和一些型号相同 的白色等腰直角三角形地砖按如图所示方式排列.

(1) 若排列正方形地砖40块,则需使用三角形地砖____________块;
(2) 若排列三角形地砖2 020块,则需使用正方形地砖____________块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,老师给出了如下问题:

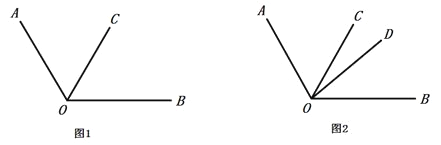
(1)以下是小刚的解答过程,请你将解答过程补充完整:
解:如图2,因为
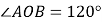 ,
,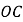 平分
平分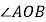 ,
,所以
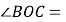 ______
______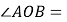 ______
______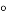 (角平分线的定义).
(角平分线的定义).因为
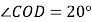 ,
,所以
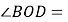 ______
______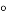 .
.(2)小戴说:“我觉得这道题有两种情况,小刚考虑的是
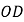 在
在 内部的情况,事实上,
内部的情况,事实上,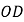 还可能在
还可能在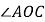 的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出
的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出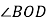 的度数:______.
的度数:______. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
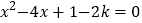 有两个不相等的实数根.
有两个不相等的实数根.(1)求k的取值范围;
(2)若k取小于1的整数,且此方程的解为整数,则求出此方程的两个整数根;
(3)在(2)的条件下,二次函数
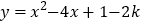 与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60,直接写出D点的坐标.
与x轴交于A、B两点(A点在B点的左侧),D点在此抛物线的对称轴上,若∠DAB=60,直接写出D点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学单元测试,七年级第一小组共10名同学,小组长把超过班级平均分的部分记为“+”,不足的部分记为“-”,记录如表:
与平均分的差值(分)
-15
-9
0
+3
+12
+17
人数
1
2
1
2
3
1
根据表格数据解答下列问题:
(1)第一小组同学的平均分比班级平均分高还是低?高或低多少分?
(2)若该班这次测试的平均分为80分,求第一小组10名同学的总分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
-
科目: 来源: 题型:
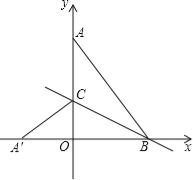
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为 .
相关试题

