搜索
【题目】阅读：一般地，一个二元一次方程ax＋by＝c (a、b、c为常数，且a、b均不为0)有无数组解，我们规定：将其每一个解中x、y的值分别作为一个点的横、纵坐标描点在平面直角坐标系中，这样我们就得到了二元一次方程的图像：一条直线。即二元一次方程的解均满足其对应直线上点的坐标：反之直线上点的坐标均为其对应的二元一次方程的解。如2x －y = 0其中一解x＝1，y＝2则对应其图像上一点（1,2）.
（1）如图，4x＋3y＝12的图像为直线m，其与x轴交点A的坐标为 ；其 与 y轴交点B的坐标为 ；
（2如图，ax＋by＝﹣5的图像为直线n，其与x轴交于C（
，0），与（1）中直线m交于P，若点P的横坐标为1 ，求a和b的值.
参考答案：
【答案】（1）
，
；（2）
.
【解析】
（1）分别令
中
、
求出与之相对应的
、
值，由此即可得出点
、
的坐标；
（2）将
代入中求出值，即可得出点
的坐标，由点
、的坐标,利用待定系数法即可求出
、
的值．
解：（1）令中，则
，
解得：
，
；
令中，则
，
解得：
，
∴
．
故答案为：；．
（2）令中，
则
，解得：
，
．
将
，
、
代入
中，
得：
，
解得：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，长青化工厂与A、B两地有公路、铁路相连．这家工厂从A地购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到B地．已知公路运价为1.5元/（吨·千米），铁路运价为1.2元/（吨·千米），且这两次运输共支出公路运输费15000元，铁路运输费97200元．
求：（1）该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？
（2）这批产品的销售款比原料费与运输费的和多多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】从三角形（不是等腰三角形）一个顶点引出一条射线于对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．
（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．
（3）如图2，△ABC中，AC=2，BC=
，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．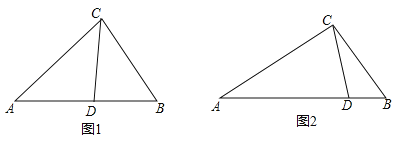
-
科目： 来源： 题型：
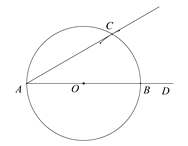
查看答案和解析>>【题目】下面是“作一个角等于30°”的尺规作图过程．
作法：如图，（1）作射线AD；
（2）在射线AD上任意取一点O（点O不与点A重合）；
（3）以点O为圆心，OA为半径作⊙O，交射线AD于点B；
（4）以点B为圆心，OB为半径作弧，交⊙O于点C；
（5）作射线AC．
∠DAC即为所求作的30°角．
请回答：该尺规作图的依据是_________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】缆车，不仅提高了景点接待游客的能力，而且解决了登山困难者的难题．如图，当缆车经过点A到达点B时，它走过了700米．由B到达山顶D时，它又走过了700米．已知线路AB与水平线的夹角
为16°，线路BD与水平线的夹角β为20°，点A的海拔是126米．求山顶D的海拔高度（画出设计图，写出解题思路即可）．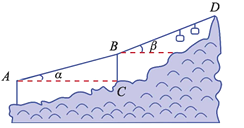
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系中，已知点
，
，
，a是
的立方根，方程
是关于x，y的二元一次方程，d为不等式组
的最大整数解．
求点A、B、C的坐标；
如图1，若D为y轴负半轴上的一个动点，当
时，
与
的平分线交于M点，求
的度数；
如图2，若D为y轴负半轴上的一个动点，连BD交x轴于点E，问是否存在点D，使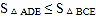
？若存在，请求出D的纵坐标
的取值范围；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，函数y=
（k＞0，x＞0）的图象与直线y=2x﹣2交于点Q（2，m）．（1）求m，k的值；
（2）已知点P（a，0）（a＞0）是x轴上一动点，过点P作平行于y轴的直线，交直线y=2x﹣2于点M，交函数y=
的图象于点N．①当a=4时，求MN的长；
②若PM＞PN，结合图象，直接写出a的取值范围．
相关试题
