[题目]如图.已知∠1+∠2=180°.∠A=∠C.DA平分∠BDF.试说明BC平分∠DBE. 题目和参考答案 ——青夏教育精英家教网—

【题目】如图，已知∠1＋∠2=180°，∠A=∠C，DA平分∠BDF，试说明BC平分∠DBE.

参考答案：

【答案】证明见解析

【解析】试题分析：由∠2＋∠BDC=180°，∠1＋∠2=180°可得∠BDC=∠1，所以AE∥FC，所以∠EBC=∠C，又因为∠A=∠C，所以∠EBC=∠A，所以AD∥BC，所以∠ADB=∠CBD，

∠ADF=∠C，所以∠ADF=∠EBC，又因为DA平分∠BDF，所以∠ADB=∠ADF，所以∠CBD=∠EBC，所以BC平分∠DBE．

试题解析：

证明：∵∠2＋∠BDC=180°，∠1＋∠2=180°，

∴∠BDC=∠1，

∴AE∥FC，

∴∠EBC=∠C，

又∵∠A=∠C，

∴∠EBC=∠A，

∴AD∥BC，

∴∠ADB=∠CBD，∠ADF=∠C，

∴∠ADF=∠EBC，

又∵DA平分∠BDF，

∴∠ADB=∠ADF，

∴∠CBD=∠EBC，

∴BC平分∠DBE．

相关试题

科目： 来源： 题型：

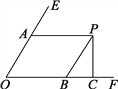
【题目】如图所示，∠EOF=60°，PA∥OF，PB∥OE，PC⊥OF于点C，求∠BPC的度数．
查看答案和解析>>
科目： 来源： 题型：

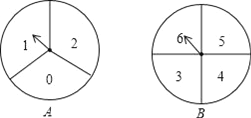
【题目】如图，小华和小丽两人玩游戏，她们准备了A、B两个分别被平均分成三个、四个扇形的转盘．游戏规则：小华转动A盘、小丽转动B盘．转动过程中，指针保持不动，如果指针恰好指在分割线上，则重转一次，直到指针指向一个数字所在的区域为止．两个转盘停止后指针所指区域内的数字之和小于6，小华获胜．指针所指区域内的数字之和大于6，小丽获胜．
（1）用树状图或列表法求小华、小丽获胜的概率；
（2）这个游戏规则对双方公平吗？请判断并说明理由．
查看答案和解析>>
科目： 来源： 题型：

【题目】若（x2+x+b）（2x+c）＝2x3+7x2﹣x+a，则a，b，c的值分别为（　　）
A.a＝﹣15，b＝﹣3，c＝5B.a＝﹣15，b＝3，c＝﹣5
C.a＝15，b＝3，c＝5D.a＝15，b＝﹣3，c＝﹣5
查看答案和解析>>
科目： 来源： 题型：

【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．
【特例探究】
（1）如图1，当tan∠PAB=1，c=4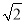时，a=　　，b=　　；
如图2，当∠PAB=30°，c=2时，a=　　，b=　　；
【归纳证明】
（2）请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．
【拓展证明】
（3）如图4，ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3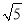，AB=3，求AF的长．
查看答案和解析>>
科目： 来源： 题型：

【题目】一块长105m、宽60m的长方形土地如下图所示．
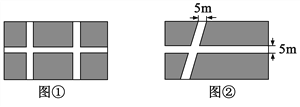
(1)上面修了两条平行且与第三条垂直的小路，宽都是5m，如图①，将阴影部分种上草坪，则草坪的面积是多少？
(2)小明在解决问题后发现：把小路改为如图②所示的平行四边形的形状，草坪的面积不变，你同意他的观点吗？为什么？
查看答案和解析>>
科目： 来源： 题型：

【题目】抛物线y＝2(x﹣1)2﹣3向左平移2个单位，再向上平移5个单位，所得的抛物线的解析式为(　　)
A.y＝2(x+1)2+2B.y＝2(x﹣1)2+2
C.y＝2(x+1)2﹣2D.y＝2(x﹣1)2﹣2
查看答案和解析>>