【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.

参考答案:
【答案】(1)![]() ;(2)10.
;(2)10.
【解析】试题分析:(1)当a=90时,b=40,求出侧面积,利用配方法求纸盒侧面积的最大值;
(2)根据题意列方程求解即可.
试题解析:
(1)S侧=2[x(90-2x)+x(40-2x)] =-8x2+260x
=-8(x-![]() )2+
)2+![]() .
.
∵-8<0,∴当x=![]() 时,S侧最大=
时,S侧最大=![]() .
.
(2)设EF=2m,则EH=7m,
则侧面积为2(7mx+2mx)=18mx,底面积为7m·2m=14m,
由题意,得18mx:14m=9:7,∴m=x.
则AD=7x+2x=9x,AB=2x+2x=4x
由4x·9x=3600,且x>0,
∴x=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
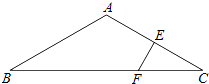
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据4,3,5,3,6,3,4的众数和中位数是( )
A.3,4B.3,5C.4,3D.4,5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.
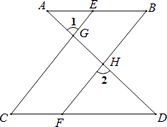
理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD()
∴∠2=∠CGD(等量代换)
∴CE∥BF()
∴∠=∠BFD()
又∵∠B=∠C(已 知)
∴(等量代换)
∴AB∥CD() -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.
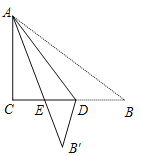
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:四边形ABCD∽四边形A′B′C′D′,它们的周长分别为5m和3m,则S四边形ABCD:S四边形A′B′C′D′=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(-3,5)关于原点对称的点的坐标为( )
A.(– 3,–5)B.(3,5)C.(–3,5)D.(3,–5)
相关试题

