【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=8,BO=DO=6,点P为线段AC上的一个动点。

⑴ 填空:AD=CD=_____ .
⑵ 过点P分别作PM⊥AD于M点,作PH⊥DC于H点.连结PB,在点P运动过程中,PM+PH+PB的最小值为____________.
参考答案:
【答案】10 15.6
【解析】
(1)在△AOD中,由勾股定理可求得AD=10,由AC⊥BD,AO=CO,可知DO是AC的垂直平分线,由线段垂直平分线的性质可知AD=CD=10;
(2)连接DP,根据题意可知S△ADP+S△CDP=S△ADC,由三角形的面积公式可知![]() ADPM+
ADPM+![]() DCPH=
DCPH=![]() ACOD,将AC、OD、AD、DC的长代入化简可知PM+PH为定值9.6,当PB最短时,PM+PH+PB有最小值,由垂线的性质可知当点P与点O重合时,PB有最小值6,即可得解.
ACOD,将AC、OD、AD、DC的长代入化简可知PM+PH为定值9.6,当PB最短时,PM+PH+PB有最小值,由垂线的性质可知当点P与点O重合时,PB有最小值6,即可得解.
解:(1)∵AC⊥BD于点O,
∴△AOD为直角三角形.
∴AD=![]() =
=![]() =10.
=10.
∵AC⊥BD于点O,AO=CO,
∴AD=CD=10;
(2)如图所示:连接PD,

∵S△ADP+S△CDP=S△ADC,
∴![]() ADPM+
ADPM+![]() DCPH=
DCPH=![]() ACOD,即
ACOD,即![]() ×10×PM+
×10×PM+![]() ×10×PH=
×10×PH=![]() ×16×6,
×16×6,
∴10×(PM+PH)=16×6,
∴PM+PH=9.6,
∴当PB最短时,PM+PH+PB有最小值.
∵由垂线段最短可知:当BP⊥AC时,PB最短,
∴当点P与点O重合时,PM+PH+PB有最小,最小值=9.6+6=15.6.
故答案为:(1)10;(2)15.6.
-
科目: 来源: 题型:
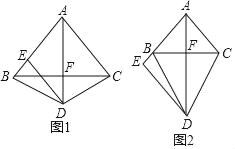
查看答案和解析>>【题目】如图1,已知△ABC中,AB=AC,点D是△ABC外一点(与点A分别在直线BC两侧),且DB=DC,过点D作DE∥AC,交射线AB于E,连接AE交BC于F.
(1)求证:AD垂直BC;
(2)如图1,点E在线段AB上且不与B重合时,求证:DE=AE;
(3)如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加快“秀美荆河水系生态治理工程”进度,污水处理厂决定购买10台污水处理设备.现有A,B两种型号的设备,每台的价格分别为a万元,b万元,每月处理污水量分别为240吨,200吨.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值;
(2)厂里预算购买污水处理设备的资金不超过105万元,你认为有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为污水处理厂设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】几何探究题
(1)发现:在平面内,若BC=a,AC=b,其中a>b.
当点A在线段BC上时(如图1),线段AB的长取得最小值,最小值为 ;
当点A在线段BC延长线上时(如图2),线段AB的长取得最大值,最大值为 .
(2)应用:点A为线段BC外一动点,如图3,分别以AB、AC为边,作等边△ABD和等边△ACE,连接CD、BE.
①证明:CD=BE;
②若BC=3,AC=1,则线段CD长度的最大值为 .
(3)拓展:如图4,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线AB外一动点,且PA=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级数学兴趣小组的同学调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图。依据图中信息,解答下列问题:

(1)接受这次调查的家长共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“很赞同”的家长占被调查家长总数的百分比是 ;
(4)在扇形统计图中,“不赞同”的家长部分所对应扇形的圆心角度数是 度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.
 (保留作图痕迹,不要求写作法和证明);
(保留作图痕迹,不要求写作法和证明);(2)在(1)条件下,连结BD,当BC=3cm,AB=5cm时,求△BCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,点
中,点 在
在 边所在直线上(与点
边所在直线上(与点 ,
, 不重合),点
不重合),点 在
在 边所在直线上,且
边所在直线上,且 ,
, 交
交 边于点
边于点 .
.
(1)如图1,若
 是等边三角形,点
是等边三角形,点 在
在 边上,过点
边上,过点 作
作 于
于 ,试说明:
,试说明: .
.某同学发现可以由以下两种思路解决此问题:
思路一:过点
 作
作 ,交
,交 于点
于点 ,如图1
,如图1因为
 是等边三角形,得
是等边三角形,得 是等边三角形
是等边三角形又由
 ,得
,得

再说明


得出
 .
.从而得到结论.
思路二:过点
 作
作 ,交
,交 的延长线于点
的延长线于点 ,如图
,如图
①请你在“思路一”中的括号内填写理由;
②根据“思路二”的提示,完整写出说明过程;
(2)如图3,若
 是等腰直角三角形,
是等腰直角三角形, ,点
,点 在线段
在线段 的延长线上,过点
的延长线上,过点 作
作 于
于 ,试探究
,试探究 与
与 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
相关试题

