【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS.下列结论:①点P在∠A的角平分线上;②AS=AR;③QP∥AR;④△BRP≌△QSP.其中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】∵△ABC是等边三角形,PR⊥AB,PS⊥AC,且PR=PS,∴P在∠A的平分线上,故①正确;
由①可知,PB=PC,∠B=∠C,PS=PR,∴△BPR≌△CPS,∴AS=AR,故②正确;
∵AQ=PQ,∴∠PQC=2∠PAC=60°=∠BAC,∴PQ∥AR,故③正确;
由③得,△PQC是等边三角形,∴△PQS≌△PCS,又由②可知,④△BRP≌△QSP,故④也正确,∵①②③④都正确,故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了两幅统计图:
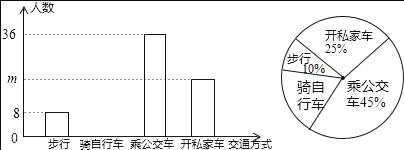
(1)样本中的总人数为 人;扇形统计十图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有1000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.

-
科目: 来源: 题型:
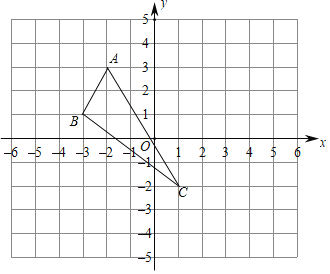
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点的位置如图所示.
(1)若△ABC内有一点P(a,b)随着△ABC平移后到了点P′(a+4,b﹣1),直接写出A点平移后对应点A′的坐标.
(2)直接作出△ABC关于y轴对称的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点)
(3)求四边形ABC′C的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.
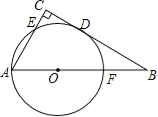
(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.
(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.
-
科目: 来源: 题型:
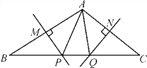
查看答案和解析>>【题目】如图所示,MP和NQ分别垂直平分AB和AC.
(1)若△APQ的周长为12,求BC的长;
(2)∠BAC=105°,求∠PAQ的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:
 ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈3.16)
≈3.16)
相关试题

