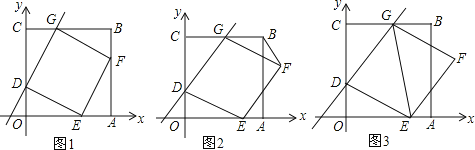
【题目】在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.
(1)如图1,顶点F在边AB上,当CG=OD时,
求m的值;
菱形DEFG是正方形吗?如果是请给予证明.
(2)如图2,连接BF,设CG=a,△FBG的面积为S,求S与a的函数关系式;
(3)如图3,连接GE,当GD平分∠CGE时,请直接写出m的值.
参考答案:
【答案】(1)m=2证明见解析(2)①2;6﹣a(3)m=![]()
【解析】试题分析:(1)将x=0代入y=mx+2得y=2,故此点D的坐标为(0,2),由CG=OD=2可知点G的坐标为(2,6),将点G(2,6)代入y=mx+2可求得m=2;
(2)如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.先证明Rt△GHF≌Rt△EOD,从而得到FH=DO=2,由三角形的面积公式可知:S=6-a.
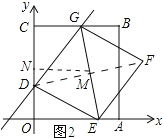
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.由菱形的性质可知:DM⊥GM,点M为DF的中点,根据角平分线的性质可知:MD=CD=4,由中点坐标公式可知点M的纵坐标为3,于是得到ND=1,根据勾股定理可求得MN=![]() ,于是得到点M的坐标为(
,于是得到点M的坐标为(![]() ,3)然后利用待定系数法求得DM、GM的解析式,从而可得到点G的坐标,最后将点G的坐标代入y=mx+2可求得m=
,3)然后利用待定系数法求得DM、GM的解析式,从而可得到点G的坐标,最后将点G的坐标代入y=mx+2可求得m=![]() .
.
解:(1)∵将x=0代入y=mx+2得;y=2,∴点D的坐标为(0,2).
∵CG=OD=2,∴点G的坐标为(2,6).
将点G(2,6)代入y=mx+2得:2m+2=6.解得:m=2.
证明△DOE≌△GCD(HL),再证明∠GDE=90°,即可证出菱形GDEF为正方形.
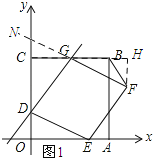
(2)①如图1所示:过点F作FH⊥BC,垂足为H,延长FG交y轴与点N.
∵四边形DEFG为菱形,∴GF=DE,GF∥DE.∴∠GNC=∠EDO.
∴∠NGC=∠DEO.∴∠HGF=∠DEO.
在Rt△GHF和Rt△EOD中,
 ,
,
∴Rt△GHF≌Rt△EOD.∴FH=DO=2.
∴![]() =
=![]() ×2×(6﹣a)=6﹣a.
×2×(6﹣a)=6﹣a.
(3)如图2所示:连接DF交EG于点M,过点M作MN⊥y轴,垂足为N.
又∵四边形DEFG为菱形,
∴DM⊥GM,点M为DF的中点.
 ∵GD平分∠CGE,DM⊥GM,GC⊥OC,
∵GD平分∠CGE,DM⊥GM,GC⊥OC,
∴MD=CD=4.
∵由(2)可知点F的坐标为4,点D的纵坐标为2,
∴点M的纵坐标为3.
∴ND=1.
在Rt△DNM中,MN=![]() =
=![]() .
.
∴点M的坐标为(![]() ,3).
,3).
设直线DM的解析式为y=kx+2.将(![]() ,3)代入得:
,3)代入得:![]() k+2=3.
k+2=3.
解得:k=![]() .
.
∴设直线MG的解析式为y=![]() x+b.将(
x+b.将(![]() ,3)代入得:﹣15+b=3.
,3)代入得:﹣15+b=3.
解得:b=18.
∴直线MG的解析式为y=﹣![]() x+18.
x+18.
将y=6代入得:![]() .
.
解得:x=![]() .
.
∴点G的坐标为(![]() ,6).
,6).
将(![]() ,6)代入y=mx+2得:
,6)代入y=mx+2得:![]() m+2=6.
m+2=6.
解得:m=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业今年8月的产值为a万元, 9月份比8月份增加了10%,10月份比9月份增加了15%,则10月份的产值是( )
A.a(1 10%)(1 15%)万元B.(a 10%)(a 15%)万元
C.a(1 90%)(1 85%)万元D.a(1 10% 15%)万元
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填入相应的大括号
﹣5,|﹣
 |,0,﹣3.14,
|,0,﹣3.14,  ,﹣12,0.1010010001…,+1.5,﹣30%,﹣(﹣6),﹣
,﹣12,0.1010010001…,+1.5,﹣30%,﹣(﹣6),﹣
正有理数集合:{________…}
非正整数集合:{________…}
负分数集合:{________…}
无理数集合:{________…}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;…;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.
(1)如图1,矩形ABCD中,若AB=3,BC=9,则称矩形ABCD为 阶奇异矩形.
(2)如图2,矩形ABCD长为7,宽为3,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(3)已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方直接写出a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】庆祝中华人民共和国成立70周年阅兵式于2019年10月1日在天安门广场隆重举行,此次阅兵约9万人参与演练及现场保障工作,将数据9万用科学记数法表示为( )
A.9×103B.9×104C.9×105D.9×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后
 点D与点B重合,点C落在点
点D与点B重合,点C落在点 的位置上
的位置上 若
若 .
.
 求
求 、
、 的度数;
的度数; 求长方形纸片ABCD的面积S.
求长方形纸片ABCD的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】【再现】如图①,在△ABC中,点D,E分别是AB,AC的中点,可以得到:DE∥BC,且DE=
 BC.(不需要证明)
BC.(不需要证明)【探究】如图②,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,判断四边形EFGH的形状,并加以证明.
【应用】在(1)【探究】的条件下,四边形ABCD中,满足什么条件时,四边形EFGH是菱形?你添加的条件是: .(只添加一个条件)
(2)如图③,在四边形ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点,对角线AC,BD相交于点O.若AO=OC,四边形ABCD面积为5,则阴影部分图形的面积和为 .

相关试题

